What is Pascal Law?
Pascal law is commonly known as “Pascal law for transmission of liquid pressure”.
It can be stated in different ways as –
- The pressure exerted at any point on an enclosed liquid is transmitted equally in all directions.
- A change in pressure applied to an enclosed in-compressible fluid is transmitted undiminished to every point of the fluid and the walls of the containing vessel.
- The pressure in a fluid at rest is same at all points if gravity is ignored.
Proof of Pascal law
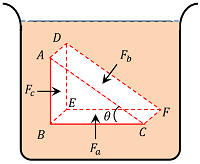
Consider a small right angled prismatic element ABCDEF in the interior of a fluid mass at rest.
The element ABCDEF is so small that all its faces and points can be assumed to be at same depth from the liquid surface. Therefore, the effect of gravity is same for all of its points.
Suppose, the fluid exerts pressure ( P_a ), \ ( P_b ) \ \& \ ( P_c ) on the faces BEFC, \ ADFC \ \& \ ADEB respectively and the corresponding normal forces on these faces are ( F_a ), \ ( F_b ) \ \& \ ( F_c ) .
Let, ( A_a ), \ ( A_b ) \ \& \ ( A_c ) are the respective areas of the three faces.
In right angled triangle ( \triangle ABC ) let ( \angle ACB = \theta ) .
As the prismatic element is in equilibrium within the fluid mass then by Newton’s law, the fluid force should balance in various directions.
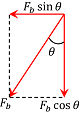
- Along horizontal direction ( F_b \sin \theta ) = F_c
- Along vertical direction ( F_b \cos \theta ) = F_a
From the geometry of the figure, we get –
( A_b \sin \theta ) = A_c \quad \text {and} \quad ( A_b \cos \theta ) = A_a
From the above equations, we get \left ( \frac {F_b \sin \theta}{A_b \sin \theta} \right ) = \left ( \frac {F_c}{A_c} \right )
And, \quad \left ( \frac {F_b \cos \theta}{A_b \cos \theta} \right ) = \left ( \frac {F_a}{A_a} \right )
- Therefore, \quad \left ( \frac {F_a}{A_a} \right ) = \left ( \frac {F_b}{A_b} \right ) = \left ( \frac {F_c}{A_c} \right )
So, \quad P_a = P_b = P_c
Hence, pressure exerted is same in all directions in a fluid at rest.
- This proves the Pascal’s law of transmission of fluid pressure.
Applications of Pascal Law
Various applications of Pascal’s law are discussed below –
Hydraulic lift & Hydraulic press
Hydraulic lift is used to lift heavy loads or press heavy objects. It is a force multiplier. It works on the principle of multiplication of thrust.
A hydraulic lift is consists of two cylinders C_1 and C_2 connected to each other by a pipe. The cylinders are fitted with water-tight friction-less pistons of different cross sectional area. The cylinders and pipe contain a liquid.
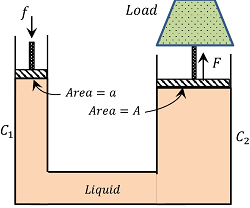
Let, a force ( f ) is applied on the smaller piston of cross-sectional area ( a ) . Then pressure exerted on the liquid –
P = \left ( \frac {f}{a} \right )
Principle of multiplication of thrust
According to Pascal’s law, the same pressure ( P ) is also transmitted to the larger piston of cross-sectional area ( A ) .
Therefore, force on larger piston will be –
F = P \times A = \left ( \frac {f}{a} \right ) \times A
Or, \quad F = \left ( \frac {A}{a} \right ) \times f
Since, \quad ( A > a ) \quad . Therefore, \quad ( F > f ) .
Hence, by making the ratio \left ( \frac {A}{a} \right ) larger very heavy loads (like cars and trucks etc.) can be lifted by the application of a much smaller force.
In this way, a small force which is applied to the small piston results a huge multiplied thrust at the large piston. This is called principle of multiplication of thrust.
- There is an increase in liquid thrust. However, there is no gain in work done by the liquid.
From principle of conservation of energy –
The work done by the force ( f ) on piston ( P_1 ) is equal to the work output at piston ( P_2 ) .
Let, the piston ( P_1 ) moves a distance ( x_1 ) and the distance moved by piston ( P_2 ) is ( x_2 )
Then volume of liquid displaced by piston ( P_1 ) is equal to volume of liquid displaced by piston ( P_2 ) .
Or, \quad a \times ( x_1 ) = A \times ( x_2 )
Or, \quad \left ( \frac {A}{a} \right ) = \left ( \frac {x_1}{x_2} \right )
Hence, increased thrust at piston ( P_2 ) is the resulted due to increased distance moved by the piston ( P_1 ) .
Hydraulic brakes
The hydraulic brakes used in automobiles are based on “Pascal law of transmission of pressure” in a liquid.
A hydraulic brake consists of a tube ( T ) containing brake oil. One end of this tube is connected to a master cylinder fitted with piston ( P ) . The piston ( P ) is attached to the brake pedal through a lever system. The other end of the tube is connected to the wheel cylinder having two pistons ( P_1 ) and ( P_2 ) .
The pistons ( P_1 ) and ( P_2 ) are connected to the brake shoes ( S_1 ) and ( S_2 ) respectively. The area of cross-section of the wheel cylinder is larger than that of master cylinder.

When the pedal is pressed, its lever system pushes the piston ( P ) into the master cylinder. The pressure is transmitted through the oil to the pistons, ( P_1 ) and ( P_2 ) in the wheel cylinder. The pistons ( P_1 ) and ( P_2 ) are pushed outwards. The brake shoes ( S_1 ) and ( S_2 ) get pressed against the inner rim of the wheel retarding the motion of the wheel. As the cross-sectional area of wheel cylinder is larger than that of master cylinder, a small force applied to the pedal produces a large retarding force on wheels.
When the pedal is released, a returning spring pulls the brake shoes away from the rim and release the brakes. The pistons ( P_1 ) and ( P_2 ) move towards their normal positions and the oil is forced back into the master cylinder.
