Fluid Pressure

What is called fluid pressure?

The fluid pressure at a point on a surface in contact with a liquid is the thrust acting normally per unit area around that point.

Let, a total force or thrust ( F ) of a liquid acts normally over a flat surface of area ( A ) . Then, the fluid pressure is given by –

\text {Pressure} = \frac {\text {Normal force}}{\text {Area of surface}}

= \left ( \frac {F}{A} \right )

• In CGS system, unit of pressure is \text {gm-cm}^{-2}
• In SI system, unit of pressure is \text {kg-m}^{-2}
• Other familiar units of pressure are \text {Pascal ( Pa ), bar, psi, mm or cm of mercury} etc.

Expression for fluid pressure

Consider a liquid at rest in a container as shown in figure. Now consider a cylindrical liquid body mass of cross sectional area, ( A ) and height ( h ) as shown in figure. Since the cylindrical element of the liquid is in equilibrium, as per Pascal law, the liquid pressure must be same at all points which are at the same depth.

Let, ( P_1 ) and ( P_2 ) be the liquid pressures at its top face 1 and bottom face 2 respectively.

Various forces acting on liquid cylinder in vertical direction are –

1. Force due to the liquid pressure at the top ( F_1 = P_1 A ) (This is acting downwards)
2. Force due to the liquid pressure at the bottom ( F_2 = P_2 A ) (This is acting upwards)
3. Weight of the liquid cylinder acting downwards ( W = \text {Mass} \ \times g = \text {Volume} \ \times \ \text {density} \ \times \ g = A h \rho g ) ( where ( \rho ) is the density of the liquid ).

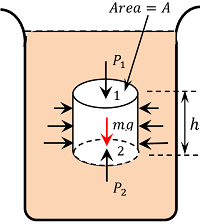
As the liquid cylinder is in equilibrium –

• Therefore, \quad \text {Net downward force} = \text {Net upward force}

So, \quad F_1 + W = F_2

Or,  \quad F_2 - F_1 = W

So,  \quad P_2 A - P_1 A = W = A h \rho g

• Thus, \quad ( P_2 - P_1 ) = h \rho g

Absolute pressure

Total pressure of liquid at certain depth ( h ) from the free surface of the liquid is called absolute pressure.

If the top face 1 of the cylinder coincides with the liquid open surface to the atmosphere, then we have –

P_1 = P_a ( i.e. atmospheric pressure )

Let, \quad P_2 is expressed by ( P ) [ i.e. pressure of liquid at any depth ( h ) from free surface ] –

Then, \quad ( P - P_a ) = h \rho g

• Therefore, \quad P = ( P_a + h \rho g )

This gives an expression for total pressure of liquid at certain depth ( h ) .

Gauge pressure

At a depth ( h ) of a liquid, the pressure is ( P ) and, at the free surface it is ( P_a )

By the expression of pressure \quad P = ( P_a + h \rho g ) \quad .

It is noted that  \quad P > P_a

The excess pressure of magnitude ( P - P_a  ) , is called gauge pressure of liquid at a depth ( h ) from the free surface.

Therefore, gauge pressure \quad ( P - P_a ) = h \rho g

From this expression, we can note the following points –

1. The liquid pressure is the same at all points at the same horizontal level or at same depth.
2. Pressure at any point inside the fluid depends upon the depth ( h ) .
3. The absolute (actual) pressure ( P ) at a depth ( h ) below the liquid surface which is open to the atmosphere is greater than the atmospheric pressure by an amount \left ( h \rho g \right ) .

Therefore, at a point in the liquid body, pressure –

1. – does not depend upon cross-section area or base area of a vessel.
2. – only depends upon the depth of liquid at the point under consideration.
3. – does not depend upon shape of a vessel.

Pressure head

From the above discussions, in a liquid body at a depth h from its free surface –

The absolute pressure \quad P = ( P_a+ h \rho g )

And, gauge pressure \quad ( P - P_a ) = h \rho g

In the above expressions density ( \rho ) is constant for a given liquid. Therefore, it is obvious that the pressure can be expressed in either of the following two ways –

1. Pressure can be expressed as a force per unit area in \text {kg-cm}^2, \ \text {kg-m}^2 \ \text {or N-mm}^2, \ \text {N-m}^2 \ \text {or Pascal} ( Pa )
2. Pressure can be expressed as a height of the equivalent liquid column whose unit may be \text {mm}, \ \text {cm} \ \text {or m} .

Thus, expressing gauge pressure of liquid in terms of height of equivalent liquid column is called pressure head.

If, P is the gauge pressure at a certain depth ( h ) of the liquid from the free surface –

Then, \quad P = h \rho g

Or, pressure head \quad h = \left ( \frac {P}{\rho g} \right )

Pressure measurement

Various types of fluid pressure measuring equipment are in use. These are –

1. Torricelli’s barometer.
2. Bourdon tube pressure gauge.
3. Diaphragm pressure gauge.
4. Piezometer.
5. Manometer.

Torricelli’s barometer

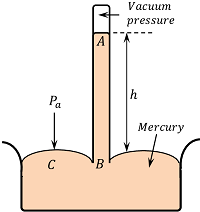
An Italian scientist E. Torricelli was first to device a method for measuring atmospheric pressure accurately. It is called a simple barometer.

A 1 \ m long glass tube closed at one end is filled with clean and dry mercury. After closing the end of the tube with the thumb, the tube is inverted into a dish of mercury as shown in figure. When thumb is removed, the mercury level in the tube falls down a little and comes to rest at a vertical height of 76 \ Cm above the mercury level in the dish.

The space above mercury in the tube is almost a perfect vacuum and is called Torricellian vacuum.

Therefore, pressure at point A is ( P_A = 0 )

Consider a point C on the mercury surface in the dish and point B in the tube at the same horizontal level. Then by Pascal’s law –

P_B = P_C = \text {Atmospheric pressure,} \ P_a

If ( h ) is the height of mercury column and ( \rho ) is the density of mercury, Then –

P_B = P_A + h \rho g

= 0 + h \rho g

= h \rho g

For a mercury barometer ( h =76 \ \text {cm} = 0.76 \ \text {m} )

And, density of mercury \quad \rho = 13.6 \times 10^3 \ \text {kg-m}^{-3}, \ g = 9.8 \ \text {m-s}^{-2}

Therefore, Atmospheric pressure \quad P_a = 0.76 \times 13.6 \times 10^3 \times 9.8 = 1.013 \times 10^5 \ Pa .

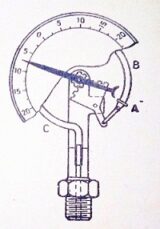
Bourdon’s tube pressure gauge

Bourdon’s pressure gauge is used to measure the pressure above or below the atmospheric pressure.

A Bourdon’s tube pressure gauge, in its simplest form, consists of an elliptical tube ABC, bent into an arc of a circle as shown in figure. This bent tube is called Bourdon’s tube.

When the gauge tube of pressure gauge is connected to the fluid (whose pressure is to be measured) at C, the fluid under pressure flows into the tube. The Bourdon’s tube as a result of the increased pressure, tends to straighten itself. Since the tube is encased in a circular cover, therefore, it tends to become circular instead of straight. With the help of a simple pinion and sector arrangement, the elastic deformation of the Bourdon’s tube rotates the pointer. This pointer moves over a calibrated scale, which directly gives the reading of pressure.

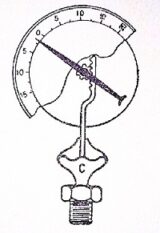
Diaphragm pressure gauge

Diaphragm pressure gauge is used to measure the pressure above or below the atmospheric pressure. A diaphragm pressure gauge, in its simplest from, consists of a corrugated diaphragm in place of Bourdon’s tube as shown in figure.

When the gauge is connected to the fluid (whose pressure is to be measured) at C, the fluid under pressure causes some deformation of the diaphragm. With the help of some pinion arrangement, the elastic deformation of the diaphragm rotates the pointer. This pointer moves over a calibrated scale, which directly gives the reading of pressure.

A diaphragm pressure gauge is generally used to measure relatively low pressures whereas a Bourdon’s pressure gauge is used for measuring high pressures.

See numerical problems based on this article.

• P040101
• P070103