What is Gravitational Force?
In universe, all bodies attract to other bodies with a force of attraction called force of gravitation or gravitational force. This force of attraction depends upon the mass of interacting bodies and the distance between them.
Therefore, gravitational force is the force of attraction between any two bodies in the universe by virtue of their masses.
Gravity
When earth is one of the bodies between two interacting bodies resulting in gravitational force of attraction between them, then the force of attraction is called gravity.
Therefore, gravity is the force of attraction by which earth attracts any object lying on its surface or near to its surface.
Features of Gravitational Force
Important features of gravitational forces are –
- It is a force between two masses and doesn’t depend upon the medium.
- Mutual gravitational forces between two bodies are equal and opposite, hence obeys Newton’s third law of motion.
- Law of gravitation strictly holds for point masses.
- Gravitational force is a central force which acts along the line joining centres of mass of bodies.
- The gravitational force possess spherical symmetry.
- Gravitational force is a conservative force (A conservative force is a force with the property that total work done in moving a particle between two points is not dependent on the path of movement of that particle. It depends only on the start point and end point. Therefore, total work done by a conservative force in moving a particle in a circle will comes to zero.)
- The gravitational force between two bodies is independent of presence of other bodies.
Newton’s Laws of Gravitation
Newton stated three laws for gravitational force of attraction between two interacting bodies which are commonly called as universal laws of gravitation.
These laws are stated as –
First Law of Gravitation
Newton’s first law of gravitation states that –
Gravitational force of attraction between two bodies is directly proportional to the product of their masses.
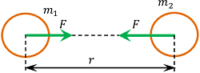
Consider about two bodies of masses ( m_1 ) \ \text {and} \ ( m_2 ) are kept at a distance ( r ) apart as shown in figure.
Therefore, \quad F \propto \left ( { m_1 }{ m_2 } \right ) ………. (1)
Second Law of Gravitation
Newton’s second law of gravitation states that –
Gravitational force of attraction between two bodies is inversely proportional to the square of the distance between them.
Therefore, \quad F \propto \left ( \frac { 1 }{ r ^2 } \right ) ……… (2)
Third Law of Gravitation
Newton’s third law of gravitation states that –
The force of gravitation acts along the line joining the centre of masses of two interacting bodies.
By combining the relations (1) and (2), we get –
F \propto \left ( \frac { m_1 m _2 }{ r^2 } \right )
Or, \quad F = G \left ( \frac {m_1 m_2 }{ r ^2 } \right )
Where ( G ) is a constant of proportionality which is popularly known as universal gravitational constant.
Universal Gravitational Constant
According to Newton’s laws of gravitation we have –
F = G \left ( \frac { m_1 m_2 }{ r^2 } \right )
If \quad ( m_1 = 1 ), \quad ( m_2 = 1 ) and \quad ( r = 1 )
Then, Universal Gravitational Constant \quad G = F
Therefore, universal gravitational constant is defined as the force of attraction between two bodies of unit masses placed at unit distance apart.
Superposition of Gravitational Force
Principal of superposition of gravitational forces states that –
The gravitational force between two masses acts independently and not influenced by the presence of other mass bodies.
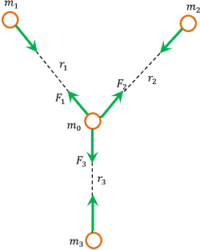
Consider about a particle of mass ( m_0 ) surrounded by three other particles of masses ( m_1 ), \ ( m_2 ) and ( m_3 ) as shown in figure.
According to the laws of gravitation –
- First force on mass ( m_0 ) exerted by the mass ( m_1 ) will be – \quad F_1 = G \left ( \frac { m_1 m_0 }{ r_1^2 } \right )
- Second force on mass ( m_0 ) exerted by mass ( m_2 ) will be – \quad F_2 = G \left ( \frac { m_2 m_0 }{ r_2^2 } \right )
- Third force on mass ( m_0 ) exerted by mass ( m_3 ) will be – \quad F_3 = G \left ( \frac { m_3 m_0 }{ r_3^2 } \right )
Therefore, resultant force ( F_R ) , acting on mass ( m_0 ) will be the vector sum of the forces ( F_1 ), \ ( F_2 ), \ \text {and} \ ( F_3 )
Or, \quad F_R = ( F_1 + F_2 + F_3 )
- In general, resultant force ( F_R ) on a particle due to the presence of ( n ) number of surrounding particles is mathematically represented as –
F_R = ( F_1 + F_2 + F_3 + ..... + F_n )
This is called principle of superposition of gravitational forces.
Newton’s Shell Theorem
Newton’s shell theorem for gravitation gives gravitational force on a point mass due to a spherical shell or a solid sphere. Shell theorem for different cases is discussed as under –
A. Gravitational Force outside shell
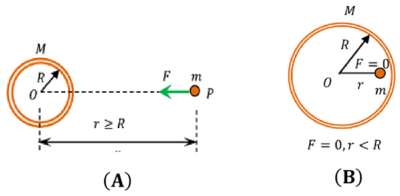
Consider that a point mass lies at point P outside of a uniform spherical shell as shown in figure (A).
- Shell has spherical symmetrical internal mass distribution.
- Then the shell attracts the point mass as if the entire mass of shell is concentrated at its centre of mass at O .
B. Gravitational Force inside shell
Consider a point mass lies inside a uniform spherical shell as shown in figure (B).
- Let, ( r ) is the distance of point mass from the centre O of the shell.
- Now consider a imaginary spherical boundary of radius ( r ) .
- There is no mass interior to this spherical boundary.
- Therefore, gravitational force on the point mass will be zero.
C. Gravitational Force outside sphere
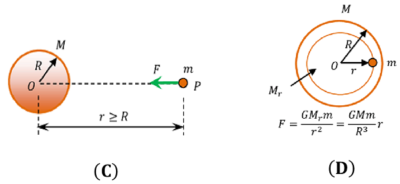
Consider that a point mass lies at point P outside a solid sphere as shown in figure (C).
- Solid sphere has homogeneous and spherical symmetric internal mass distribution.
- Then the sphere attracts the point mass as if the entire mass of sphere is concentrated at its centre of mass at O .
D. Gravitational Force inside sphere
Consider that a point mass lies inside a homogeneous solid sphere at a distance r from centre O of the sphere as shown in figure.
- The force on the point mass will act towards the centre of the sphere.
- This force is exerted by the spherical mass having radius ( r ) situated interior to the point mass.
Gravitational Shielding
Gravitational shielding is the process of preventing a body or instruments from the action of gravitational force of attraction from nearby bodies.
Consider about a particle of mass ( m_0 ) , which is kept inside a spherical shell of mass ( M ) . An other mass ( m_1 ) is present nearby outside the shell.
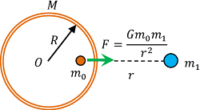
- By Newtons shell theorem, the gravitational force of attraction on the particle due to mass of the shell will be zero.
- But the particle will experience a force of attraction ( F ) due to the mass ( m_1 ) present outside the shell.
- Hence, the shell doesn’t shield the particle placed inside it from the gravitational force exerted by other mass outside of the shell.
- Thus gravitational shielding of a particle by placing inside a shell is not possible.
In this case the, gravitational force ( F ) acting on the particle is same as if shell is not present there.
Therefore, \quad F = G \left ( \frac { m_0 m_1 }{ r^2 } \right )
Thus, gravitational shielding is not possible.
See numerical problems based on this article.
