Compound Pendulum

What is called a Compound Pendulum?

A compound pendulum is a rigid body pegged and hanged freely to oscillate about a smooth horizontal axis passing through the peg.

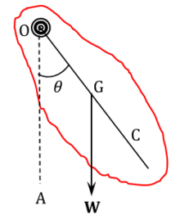
Consider about a rigid body ( compound pendulum ) as shown in figure. The rigid body is hanged through a peg at point ( O ) so that, it can oscillate freely about an horizontal axis passing through the peg ( O ) . The centre point of axis through the point ( O ) is called the centre of suspension.

In the figure, the point ( G ) is the centre of gravity of body. Now let, ( OG = h ) and ( \angle {AOG} = \theta )

Then moment of weight of body about point ( O ) will be –

M = W × OG \sin \theta = W h \sin \theta = W h \theta ( Because ( \theta ) is very small )

From definition of a torque –

\text {Moment or Torque} = \text {Moment of inertia} \times \text {Angular acceleration}

Therefore, moment of weight of the body will be –

M = \left ( \frac {W}{g} \right ) {k_0}^2 \times \left ( \frac {d^2 \theta}{dt^2} \right ) . Here, ( k_0 ) is the radius of gyration of body about ( O ) .

Hence, \quad \left ( \frac {W}{g} \right ) {k_0}^2 \times \left ( \frac {d^2 \ \theta}{dt^2} \right ) = - W h \theta

So, \quad \left ( \frac {d^2 \ \theta}{dt^2} \right ) = - \left ( \frac {g h}{k_0^2} \right ) \theta

Therefore, angular acceleration of a compound pendulum is –

\alpha = - \left ( \frac {g h}{k_0^2} \right ) \theta

But, for a given body forming the compound pendulum, the terms ( g ), \ ( h ) \ \text {and} \ ( k ) are constants. Therefore, \quad \alpha \propto \theta

Hence, the angular acceleration of body is proportional to angular displacement. Therefore, motion of body is Simple Harmonic Motion.

Time Period of Compound Pendulum

Time period of a Simple Harmonic Motion is given by –

T = 2 \pi \left ( \frac {\text {Displacement}}{\text {Acceleration}} \right )

Angular acceleration of a compound pendulum is given by –

\alpha = \left ( \frac {g h}{k_0^2} \right ) \theta

Therefore, Time period of oscillation of compound pendulum will be –

T = 2 \pi \sqrt {\left ( \frac {k_0^2}{gh} \right )} ……. (1)

A simple pendulum whose time period of oscillation is the same as that of a compound pendulum, is called its simple equivalent pendulum.

Let, ( l ) is the length of the simple equivalent pendulum, then its period of oscillation will be –

T = 2 \pi \sqrt {\left ( \frac {l}{g} \right )} ……. (2)

Hence, equating equations (1) and (2), we get –

2 \pi \sqrt {\left ( \frac {k_0^2}{gh} \right )} = 2 \pi \sqrt {\left ( \frac {l}{g} \right )}

Or, \quad l = \left ( \frac {k_0^2}{h} \right )

If, ( k ) is the radius of gyrations about a parallel axis passing through ( G ) . Then –

k_0^2 = k^2 + h^2

So, \quad l = \left ( \frac {k^2 + h^2}{h} \right )

= h + \left ( \frac {k^2}{h} \right )

Centre of Oscillation

A point ( C ) is taken on produced part of line ( OG ) , such that ( OC = l )

Then point ( C ) is called the centre of oscillation or percussion.

Therefore, \quad OC = h + \frac {k_G^2}{h}

But, \quad k_0^2 = k^2 + h^2 . Therefore, \quad k^2 = k_0^2 - h^2 = l h - h^2 = h ( l - h )

= OG ( OC - OG ) = OG \times GC

Thus, symmetry of the result shows that, if the body were suspended from a parallel axis through ( C ) , then ( O ) will become the centre of oscillation or percussion.

Hence, centre of oscillation ( C ) and point of suspension ( O ) are inter-changeable.

Conical Pendulum

One end of a string ( AO ) is attached to a fixed point ( O ) and a weight ( W ) is tied to the other end ( A ) . If the weight is made to describe a horizontal circle so that the string describes a right circular cone, whose axis is a vertical through ( O ) , then system is called a conical pendulum.

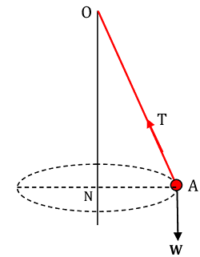
Consider about a conical pendulum as shown in figure. Let –

• ( N ) is the centre of horizontal circle of radius ( r ) described by weight.
• ( \omega ) is the angular velocity of the weight.
• ( T ) is the tension of the string.
• ( l ) is the length of the string and ( \angle {AON} = \theta )

Then \quad r = l \sin \theta

Resolving tension of the string, we will get –

1. Vertical component is \quad T \cos \theta = W …… (1)
2. Horizontal component is \quad T \sin \theta = F_C …… (2)

The horizontal component of tension provides the centripetal force ( F_C ) on the weight which is necessary to keep it moving in circle.

Then from definition of centripetal force, we have –

F_C = \left ( \frac {W}{g} \right ) \omega^2 r

Therefore, \quad T \sin \theta = \left ( \frac {W}{g} \right ) \omega^2 r = \left ( \frac {W}{g} \right ) \omega^2 l \sin \theta

So, \quad T = \left ( \frac {W}{g} \right ) \omega^2 l ……. (3)

Now dividing equation (1) by equation (3), we will get –

\cos \theta = \left ( \frac {g}{\omega^2 l} \right )

Here, ( \theta ) will be real if ( \theta < 1 )

This means that –

\left ( \frac {g}{\omega^2 l} \right ) < 1

So, \quad \omega^2 l > g

Or, \quad \omega > \sqrt {\left (\frac {g}{l} \right )}

This expression provides a necessary condition for angular velocity of a conical pendulum. It states that –

The minimum angular velocity must be \left [ \sqrt {\left ( \frac {g}{l} \right )} \right ] so that the weight may revolve in a conical pendulum. If ( \omega ) is less than this value, the string will hang vertically.

Use of Conical Pendulum

From the geometry of the figure –

ON = l \cos \theta = l \left ( \frac {g}{\omega^2 l} \right )

= l \times \left ( \frac {g}{\omega^2 l} \right ) = \left ( \frac {g}{\omega^2} \right )

So, \quad ON \propto \left ( \frac {1}{\omega^2} \right )

Therefore, the depth of weight below ( O ) is inversely proportional to the square of the angular velocity and is independent of the length of the string. Hence, it is used as a model to analyze the motion of planets.

Oscillations of a liquid column

When the surface of a liquid column kept in a U tube is displaced and released, the liquid column starts oscillating with Simple Harmonic Motion.

Consider about a U tube as shown in figure. Let –

• Cross section area of tube is ( A ) .
• Density of liquid in tube is ( \rho ) .

Height of liquid in both arms of tube is ( h ) . Mass of liquid column in the U tube will be-

m = A \times 2 h \times \rho

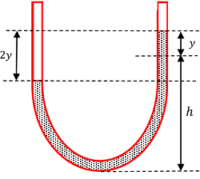
Let, the liquid in one of the arm is depressed by a distance ( y ) . Then rise of the liquid in the other arm will be the same. Therefore, total difference in height of liquid column in both arms will become ( 2y ) .

Restoring force acting on the liquid column will be –

F = Weight of unbalanced liquid column.

= - A \times 2y \times \rho \times g = - 2 A \rho g y

= - \left ( 2 A \rho g \right ) y

But, ( A ), \ ( \rho ) \ \text {and} \ ( g ) are constants. Therefore, \quad F \propto y

The force on the liquid column is proportional to the displacement and acts in opposite direction. Hence, the liquid in the tube executes Simple Harmonic Motion.

Force Constant of liquid column

Restoring force in a simple harmonic motion is given by –

F = - k y

Restoring force in a liquid column is given by –

F = - \left ( 2 A \rho g \right ) y

Comparing the equations, force constant for liquid column will be –

k = \left ( 2 A \rho g \right )

Time Period of liquid column

Time period of oscillations of liquid column will be –

T = 2 \pi \sqrt { \frac { m }{ k }}

= 2 \pi \sqrt { \frac { A \times 2 h \times \rho }{ 2 A \rho g }}

= 2 \pi \sqrt { \frac { h }{ g }}

Let, ( l )  is the total length of the liquid column. Then –

l = 2 h

Therefore, \quad T = 2 \pi \sqrt { \frac { l }{ 2 g }}