What is the First Law of Thermodynamics?
First law of thermodynamics states that –
If some heat is supplied to a system which is capable of doing work, then the quantity of heat absorbed by the system will be equal to the sum of the increase in its internal energy and the external work done by the system on the surroundings.
Consider about a thermodynamic system in which –
- ( \Delta Q ) = Heat supplied to the system by the surroundings.
- ( \Delta W ) = Work done by the system on the surroundings.
- ( \Delta U ) = Change in internal energy of the system.
Then, according to the first law of thermodynamics –
\Delta Q = ( \Delta U + \Delta W )
In a piston cylinder arrangement, the work done by the system against a constant pressure ( P ) is given by –
\Delta W = \text {Force} \ \times \ \text {Distance} = \text {Pressure} \ \times \ \text {Area} \ \times \ \text {Distance} = P \Delta V
So, the first law of thermodynamics takes the form –
\Delta Q = ( \Delta U + P \Delta V )
Sign convention in First Law of Thermodynamics
- When heat is absorbed by a system, it is taken as positive heat. When heat is removed from a system, it is taken as negative heat.
- When work is done by a system, it is taken as positive work. When work is done on the system, it is taken as negative work.
- When internal energy of a system increases, it is taken as positive energy and when it decreases, it is taken as negative energy.
Expression for Thermodynamic Work Done
Consider about a gas contained in a cylinder of cross-sectional area ( A ) as shown in figure. Let, ( P ) is the pressure of the gas.
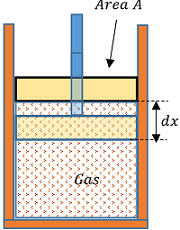
Then force exerted by the gas on the piston will be –
F = P \times A = P A
Suppose, the gas expands a little and pushes out the piston through a small distance ( dx ) .
Then work done by the gas will be –
dW = F \times dx = P A dx
Or, \quad dW = P dV
Total work done by the gas when its volume increases from ( V_1 ) to ( V_2 ) will be –
W = \int {dW} = \int\limits_{V_1}^{V_2} P \ dV
Work done in Non-Cyclic Process
A non-cyclic process is defined as that thermodynamic process in which the system does not return to its initial state.
Work done in a non-cyclic process of expansion of a gas system can be obtained by indicator diagram method. Consider about P-V indicator diagram of an expansion of a gaseous system as shown in figure.
- Points A and B represents the initial state ( P_1, \ V_1 ) and final state ( P_2, \ V_2 ) respectively of a system.
- At any instant at point a , let ( P ) and ( V ) are the pressure and volume of gas respectively.
Let, volume of the gas increases from ( V ) to ( V + dV ) corresponding to a point b on the indicator diagram such that the pressure remains constant.

Then, ad = bc = P \quad \text {and} \quad cd = dV
Therefore, small work done when the system changes from state a to state b will be –
dW = P \ dV = ad \times cd
= \text {Area of shaded strip abcd}
Therefore, total work done by the gas during the expansion from the initial state ( P_1, \ V_1 ) to the final state ( P_2, \ V_2 ) can be obtained by adding the areas of all such strips formed between AD and BC under the P-V indicator diagram.
Therefore, the total work done will be –
W = \text {Area ABCDA}
= \int\limits_{V_1}^{V_2} P \ dV = \text {Area under P-V diagram}
Hence, the work done by a system is numerically equal to the area enclosed between the P-V diagram and the volume axis.
- During expansion, the area under the P-V diagram is traced in the clockwise direction. Work is done by the gas and is taken as positive.
- During compression, the area under the P-V diagram is traced in the anticlockwise direction. Work is done on the gas and is taken as negative.
Work in a Cyclic Process
A cyclic process is defined as a thermodynamic process in which the system returns to its initial state after undergoing a series of changes.
Consider that a gas expands from the initial state A to the final state B after undergoing a series of changes of pressure and volume along the path AXB as shown in figure.
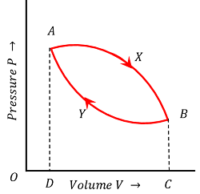
Work done by the gas during the expansion process via path AXB will be –
W_1 = \text {Area AXBCDA}
It is clockwise. Because, if we move along A \ \text {to} \ X \ \text {to} \ B \ \text {to} \ C \ \text {to} \ D \ \text {to} \ A in traversing the path of work done in process AXB , then we follow clockwise direction. Hence, it is taken as positive.
Now the gas is subjected to a compression process, so that it returns to its initial state A via the path BYA .
Work done on the gas during the compression process will be –
W_2 = \text {Area BYADCB}
It is anti-clockwise. Because, if we move along B \ \text {to} \ Y \ \text {to} \ A \ \text {to} \ D \ \text {to} \ C \ \text {to} \ B in traversing the path of work done in process BYA , then we follow an anti-clockwise direction. Hence, it is taken as negative.
Therefore, net work done during the cyclic process is –
W = ( W_1 + W_2 )
= \text {Area AXBCDA} - \text {Area BYADCB}
= \text {Area AXBYA} ( It is positive. )
Conclusion – For a cyclic process –
- Work done per cycle is numerically equal to the area of the loop representing the cycle.
- If the closed loop is traced in the clockwise direction, then the expansion curve will lie above the compression curve because ( W_1 > W_2 ) . So the area of the loop is positive which indicates that the net work is done by the system.
- If the closed loop is traced in the anticlockwise direction then the expansion curve will lie below the compression curve because ( W_1 < W_2 ) . So the area of the loop is negative which indicates that the net work is done on the system.
Zeroth Law of Thermodynamic
Zeroth law of thermodynamics states that –
If two systems ( A ) and ( B ) are in thermal equilibrium with a third system ( C ) separately then the two systems ( A ) and ( B ) must be in thermal equilibrium with each other.
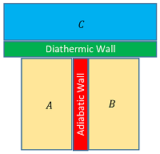
Consider about two systems ( A ) and ( B ) which are separated by an adiabatic wall ( heat will not flow ).
System ( A ) and ( B ) are separately in thermal equilibrium with a third system ( C ) as shown in figure.
The system ( C ) is separated by a diathermic or heat conducting wall from system ( A ) and ( B ) .
The system combinations, ( A ) in contact with ( C ) and ( B ) in contact with ( C ) will reach thermal equilibrium separately.
If adiabatic wall is removed, there will be no exchange of heat. This shows that systems ( A ) and ( B ) are already in thermal equilibrium with each other.
Concept of Temperature
Zeroth law of thermodynamics implies that, temperature is a physical quantity which has the same value for all system which are in thermal equilibrium with each other.
Thus, if ( A ) and ( B ) are separately in thermal equilibrium with ( C ) , then –
( T_A = T_C ) \quad \text {and} \quad ( T_B = T_C )
This shows that, \quad T_A = T_B
Hence, Zeroth law can also be expressed as – there exist a scalar quantity called temperature which is a property of all thermodynamic systems such that equality of temperature is necessary and sufficient condition for thermal equilibrium.
