Motion in Vertical Circle

What is called “Motion in a Vertical Circle”?

When a particle is made to move along a circular path in a vertical plane, the motion is a non uniform circular motion. This is due to the reason that, the particle moves under the influence of earth’s gravitational force. Hence, at every moment, the vertical height of the particle is changing and thus, the velocity of the particle and tension of the rope will be changing in magnitude at directions. This type of motion is called “motion in vertical circle”.

Analysis of motion of a particle in a vertical circle is different than the motion of particle in a circular path in horizontal plane.

Circular motion represents motion of a body in a circle laying on horizontal plane. In this case, the effect of ( g ) i.e. earth’s acceleration due to gravity is uniform over complete cycle.

Motion in vertical circle represents motion of a body in a circle laying on a vertical plane. In this case, the effect of ( g ) is changing all time over complete cycle. So, parameters of motion in vertical circle of a particle will be different than a circular motion.

Velocity at a point

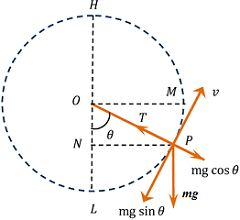
Consider about a body of mass ( m ) , tied at the end of a string and rotating in a vertical circle of radius ( r ) as shown in figure.

Suppose that, the body passes through its lowest point L with velocity ( u ) and through any other point P with velocity ( v ) .

In moving from L to P it has moved through a vertical height ( L N = h ) .

According to law of conservation of energy –

\text {Total energy at L} = \text {Total energy at P}

Or, \text {( KE + PE ) at L} = \text {( KE + PE ) at P}

Or, \quad \left ( \frac {1}{2} \right ) m u^2 + 0 = \left ( \frac {1}{2} \right ) m v^2 + m g h

Or, \quad u^2 = v^2 + 2 g h

Therefore, \quad v = \sqrt {u^2 - 2 g h} …… (1)

This equation gives linear velocity ( v ) of the body at any instant.

Tension in string

Forces acting on the body at point P are –

1. Weight of body ( mg ) – acting vertically downwards.
2. Tension of string ( T ) – acting along the string.

   

Component of weight ( mg \cos \theta ) , acts opposite to the tension ( T ) . So the net centripetal force will be –

( T - mg \cos \theta ) = \left ( \frac {mv^2}{r} \right )

Or, \quad T = \left [ mg \cos \theta + \left ( \frac {mv^2}{r} \right ) \right ] …… (2)

By geometry of figure, we have –

( \cos \theta ) = \left ( \frac {r - h}{r} \right ) …… (3)

Putting the values from equations (1) & (3) in equation (2), we will get –

T = mg \left ( \frac {r - h}{r} \right ) + \frac {m}{r} \left (u^2 - 2 g h \right )

= \left [ \left ( \frac {m}{r} \right ) \left ( u^2 + gr - 3 g h \right ) \right ] …… (4)

This equation gives tension along the string at any point of the circle.

Tension at lowest point

At the lowest point L , height is zero i.e. ( h = 0 )

Hence, tension in the string will be –

T_L = \left [ \frac {m}{r} ( u^2 + gr ) \right ] …… (5)

Tension at highest point

At the highest point H , height is ( h = 2r )

Hence, the tension in string will be –

T_H = \left ( \frac {m}{r} \right ) ( u^2 + gr - 6 gr )

= \left [ \left ( \frac {m}{r} \right ) ( u^2 - 5 gr ) \right ] …… (6)

By comparing equations (5) and (6), we get –

\text {Tension at highest point} ( T_H ) < \text {Tension at lowest point} ( T_L )

Difference in tensions

Now, difference in tensions at lowest and highest points will be –

( T_L - T_H ) = \left ( \frac {m}{r} \right ) \left [ ( u^2 + gr ) - ( u^2 - 5gr ) \right ]

= 6 mg

Thus, difference in tensions at the lowest and highest points is equal to six times of weight of revolving body.

Minimum projection velocity

The required minimum velocity at the lowest position of journey, that should be possessed by a revolving body in vertical circle, so that it go round completely without slackening in string is called Minimum projection velocity.

The body will be able to cross the highest point without any slack in the string if ( T_H ) is positive i.e. ( T_H \ge 0 )

Therefore, \quad \left ( \frac {m}{r} \right ) \left ( u^2 - 5 gr \right ) \ge 0

Or,  \quad u \ge \sqrt {5 gr}

Hence, ( \sqrt {5 gr} ) is the minimum velocity which the body must possess at the bottom of the circle so as to go round the circle completely. This phenomenon is called, looping the loop.

Critical velocity

The required minimum velocity at the highest point of journey, that should be possessed by a revolving body in vertical circle, so that it go round completely without slackening the string is called its critical velocity.

Let, ( V ) is the required minimum velocity of body, that must possess at highest point H in just to looping the loop without slackening the string, then –

  V^2 = u^2 - 2g.2r .

But, \quad u = \sqrt {5 gr}

Therefore, \quad V = \sqrt {5 gr - 4gr} = \sqrt {gr}

This gives the minimum or critical velocity at the highest point to complete the circular path.

See numerical problems based on this article.

• P030114
• P030115