What is called Linear Momentum?
Linear Momentum of a moving body is defined as the product of the mass and linear velocity of the body. It gives an idea about the energy capacity that a moving body possesses.
Concept of Momentum
To know about the concept of momentum, consider about the following consequences –
(1) Case (1) – A small piece of stone of mass ( m ) \ kg is dropped from a small height ( h ) on a glass plate kept on top of a table. It doesn’t break the glass plate.
(2) Case (2) – Now a heavy stone of mass ( 10 \ m ) \ kg is dropped from same height ( h ) on same glass plate. It is likely to break the glass plate.
(2) Case (3) – Again, same small piece of stone of mass ( m ) \ kg is now dropped from a large height ( 10 \ h ) on same glass plate, it is likely to break the glass plate.
EXPLANATION –
In case (1) – The body has low mass ( m ) and dropped from a lower height ( h ) . As such it is possessing low quantity of motion inertia and doesn’t break the glass plate.
In case (2) – The body has heavy mass of ( 10 \ m ) and dropped from a same lower height ( h ) . It is possessing about 10 times more quantity of motion inertia in comparison to Case (1) and breaks the glass plate.
In case (3) – The body has low mass ( m ) but dropped from a larger height (10 \ h ) . It is possessing about 10 times of more quantity of motion inertia in comparison to Case (1) and breaks the glass plate.
In cases (1) & (2) – Mass of body is different but since the stone is dropped from same height ( h ) , it will acquire the same velocity just at the moment of hitting the glass plate.
In cases (2) & (3) – Mass of body is same but since the stone is dropped from different heights, it will acquire a higher velocity in case (3) before hitting the glass plate.
From above discussion, we gain the concept of momentum. It is concluded that effect of motion depend on mass and velocity both. This combined effect of motion is called momentum of a moving body.
Magnitude of Momentum
Momentum is of two types –
- Linear Momentum – It is the momentum possessed by a moving body, when it is moving in linear motion i.e., motion in one dimension.
- Angular Momentum – It is the momentum possessed by a moving body, when it is moving in curve motion, circular motion or rotational motion i.e., motion in two dimensions (planer motion).
Newton’s second and third laws of motion lead to one of the most important and fundamental principles of physics, called the law of conservation of momentum.
Linear momentum of a moving body is defined as a quantity possessed by the body due to inertia of motion. Its magnitude is equal to the product of mass of body and linear velocity.
\text {Linear Momentum} = \text {Mass} \ \times \ \text {Linear Velocity}
Therefore, \quad \vec p = m \vec v
Similarly, for angular motion –
Angular momentum of a moving body is defined as a quantity possessed by the body due to inertia of motion. Its magnitude is equal to the product of mass of body and angular velocity.
\text {Angular Momentum} = \text {Mass} \ \times \ \text {Angular Velocity}
Therefore, \quad \vec L = m \vec {\omega}
Momentum is a vector quantity. Its direction is same as that of the direction of velocity of the body.
The SI unit of momentum is ( \text {kg m s}^{-1} )
Impulsive Force
A large force acting for a very short time to produce a large change in momentum is called an impulsive force.
EXAMPLES
- Force exerted by a bat while hitting a ball by cricket batsman.
- Blow of a hammer on a nail by carpenter.
- Force experienced by a person when he falls from a certain height on floor.
Impulsive force actually acts for a very short duration of time. It is difficult to measure the magnitude of force and time duration separately. But the product of force and time is a measurable quantity. This product is called an impulse.
Impulse
Impulse is the total effect of a large force which acts for a very short duration of time to produce a large change in momentum.
\text {Impulse} = \text {Force} \ \times \ \text {Time} = \text {Total change in momentum}
If ( \vec {F_{av}} ) is the average force, then –
Impulse \quad \vec {J} = \vec {F_{av}} \times \Delta t
- Impulse is a vector quantity.
- It is denoted by ( J ) .
- Its direction is same as that of the direction of force or the change in momentum.
Impulse Momentum Theorem
According to Newton’s second law of motion, we have –
\text {Applied Force} = \text {Rate of change in momentum}
Therefore, \quad \vec {F} = \left ( \frac {\vec {dp}}{dt} \right )
Or, \quad \vec {F} dt = \vec {dp} ……… (1)
Let, in time ( t = 0 ) to ( t = t ) the momentum of a body changes from ( \vec {p_1} ) to ( \vec {p_2} ) .
Then integrating equation (1) within these limits, we will get –
\int\limits_{0}^{t} \vec {F} dt = \int\limits_{\vec {p_1}}^{\vec {p_2}} \vec {dp}
= \left [ \vec {p} \right ]_{\vec {p_1}}^{\vec {p_2}}
= \vec {p_1} - \vec {p_2}
But \quad \int\limits_{0}^{t} \vec {F} dt = \vec {J} (Impulse)
Therefore, \quad \vec {J} = \vec {p_1} - \vec {p_2}
Thus, the impulse of a force is equal to the total change in momentum produced by the force.
This relationship between impulse ( \vec {J} ) and momentum ( \vec {p} ) is known as impulse-momentum theorem.
Conservation of Linear Momentum
The law of conservation of linear momentum is derived from Newton’s laws of motion. It can be stated as –
When no external force acts on a system of several interacting particles, the total linear momentum of the system is conserved. The total linear momentum is the vector sum of the linear momenta of all the particles of the system.
Consider about two bodies A \ \text {and} \ B of masses ( m_1 ) \ \text {and} \ ( m_2 ) moving in a straight line in same direction with velocities, ( u_1 ) \ \text {and} \ ( u_2 ) respectively. Let, ( u_1 > u_2 ) . After some time they will collide for very short time ( \delta t ) and after collision, let their velocities are ( v_1 ) \ \text {and} \ ( v_2 ) respectively.
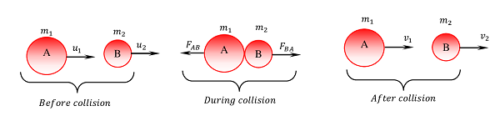
During collision, the body A will exert a force ( \vec {F_{BA}} ) on body B .
From Newton’s third law of motion, the body B will also exert a force ( \vec {F_{AB}} ) on body A .
Now, Impulse of force \quad \vec {F_{AB}} = \vec {F_{AB}} \Delta t
We know that, \quad \text {Impulse} = \text {Total change in momentum}
But, change in momentum of A is –
\left ( m_1 \vec {v_1} - m_1 \vec {u_1} \right )
Therefore, \quad \vec {F_{AB}} \Delta t = \left ( m_1 \vec {v_1} - m_1 \vec {u_1} \right )
Similarly, change in momentum of B is –
\left ( m_2 \vec {v_2} - m_2 \vec {u_2} \right )
Therefore, \quad \vec {F_{BA}} \Delta t = \left ( m_2 \vec {v_2} - m_2 \vec {u_2} \right )
According to Newton’s third law of motion –
\vec {F_{AB}} = - \vec {F_{BA}}
Therefore, \quad \left ( m_1 \vec {v_1} - m_1 \vec {u_1} \right ) = - \left ( m_2 \vec {v_2} - m_2 \vec {u_2} \right )
Or, \quad \left ( m_1 \vec {v_1} + m_2 \vec {v_2} \right ) = \left ( m_1 \vec {u_1} + m_2 \vec {u_2} \right )
Therefore, Total momentum after collision = Total momentum before collision. Hence, total momentum of the system is conserved in collision.
See numerical problems based on this article.
