What is called Centre of Mass?
The whole mass of a body may be assumed to be concentrated at a fixed point. This fixed point at which the whole mass is assumed to be concentrated, is called centre of mass of that body.
Concept of Centre of Mass
All material bodies are constructed of numerous tiny particles. These tiny particles of a body have their own masses. Hence, the total mass of the body is equal to the sum of all tiny masses by which the body is made of.
By gravitational nature of earth, each of these tiny particles is attracted towards the centre of the earth with a gravitational force, which is proportional to its mass. This is called weight of particles.
Weight of each tiny particle acts towards the centre of the earth. Therefore, these tiny weights form a system of parallel forces whose direction is towards the centre of earth. The centre of these parallel forces is called the mass centre of that body.
Consider that a body is made up of ( n ) number of tiny mass particles. Let, masses of these particles are ( m_1 ), \ ( m_2 ), \ ....... ( m_n ) etc.
Then, total mass of the whole body will be, M = ( m_1 + m_2 + ....... + m_n )
This total mass may be assumed to be acted at a single fixed point which is called “centre of mass”. In short form, it is written as COM.
Therefore, following considerations are required to understand the concept of centre of mass of a body –
- A rigid body is constructed of many small particles.
- Each tiny particle has its own mass. These tiny masses together constitute the whole mass of that body.
- The system of tiny mass particles of the body can be considered as a system of parallel forces.
- Centre of these parallel forces is the mass centre of that body.
- The centre of parallel forces or system of tiny mass particles of a body can be determined by Varignon’s theorem.
Centre of Parallel Forces
Consider about several parallel and co-planar forces P_1, \ P_2, \ ..... \ P_n etc. which are acting at different points of a body as shown in figure. Let, the co-ordinates of points are ( x_1, \ y_1 ), \ ( x_2, \ y_2 ) \ ..... \ ( x_n, \ y_n ) respectively.
The magnitude of resultant force of these forces will be ( R = \sum {P} )
Or, \quad R = ( P_1 + P_2 + \ ........ \ + P_n ) etc.
Let, the resultant ( R ) , passes through a point whose co-ordinate is ( \bar {x}, \ \bar {y} ) . This point is called “centre point of parallel forces”.
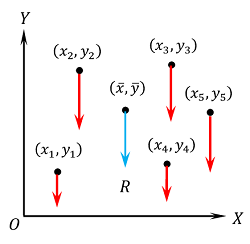
Consider that, the forces are parallel to the OY axis as shown in figure. Algebraic sum of the moments of all forces about point O will be –
\sum {P \ x} = [ ( P_1 \ x_1 ) + ( P_2 \ x_2 ) + \ ..... \ ( P_n \ x_n ) ] ……. (1)
Therefore, moment of the resultant force ( R ) about point O will be –
\left [ ( P_1 + P_2 + \ ........ \ + P_n ) \times \bar {x} \right ] ……. (2)
Since, the body remains in equilibrium, so equating equation (1) and (2), we have –
\left [ ( P_1 + P_2 + \ ..... \ + P_n ) \times \bar {x} \right ] = \left [ ( P_1 \ x_1 ) + ( P_2 \ x_2 ) + \ ..... \ ( P_n \ x_n ) \right ]
Or, \quad \bar {x} = \left [ \frac { ( P_1 \ x_1 ) + ( P_2 \ x_2 ) + \ ..... \ + ( P_n \ x_n ) }{ ( P_1 + P_2 + \ ..... \ + P_n ) } \right ] …….. (3)
Similarly, by considering the forces to be parallel to OX axis and taking moments about point O , we can evaluate –
\bar {y} = \left [ \frac { ( P_1 \ y_1 ) + ( P_2 \ y_2 ) + \ ..... \ + ( P_n \ y_n ) }{ ( P_1 + P_2 + \ ........ \ + P_n ) } \right ] ……… (4)
From equations (3) and (4), we get the co-ordinates of centre of parallel forces. These equations are commonly used to find –
- Centre of mass of objects.
- Mass centre of a system of point masses.
- The centre of gravity of solid objects.
How to find COM by Symmetry
Tiny particles of a body has its own masses. Each of these particles is attracted by the earth with a gravitational force proportional to its mass which is called weight. These tiny weights form a system of parallel forces the centre of which is called the centre of mass of that body.
Consider that, some small weights ( w_1, \ w_2, \ w_3 \ ...... ) etc. are placed on a straight line OX with their centres of gravity at distances ( x_1, \ x_2, \ x_3 \ ..... ) etc. from a fixed point O .
Therefore, total weight of system ( W = w_1 + w_2 + w_3 + ...... )
Let, the centre of gravity of total weight ( W ) , lie at a distance of ( \bar {x} ) from O .
Then, by equation (3), we get –
\bar {x} = \left ( \frac {w_1 x_1 + w_2 x_2 + ..... }{w_1 + w_2 + ..... } \right )
= \left ( \frac { \sum {w x}}{ \sum {w}} \right )
= \left ( \frac { \sum {w x}}{W} \right ) ……….. (1)
If, acceleration due to gravity at that place is ( g ) , then –
( w_1 = m_1 g, \ w_2 = m_2 g, \ w_3 = m_3 g \ ...... ) \ \text {etc. and} \ ( W = M g )
Therefore, \quad \bar {x} = \left ( \frac { \sum {m g x}}{Mg} \right )
= \left ( \frac { \sum {m x}}{M} \right ) ………… (2)
In similar manner, let a plane area ( A ) is divided into several parts whose areas are ( a_1, \ a_2, \ a_3 ) etc. and the centres of gravity of these parts lie on a straight line at distances ( x_1, \ x_2, \ x_3 ) respectively from a fixed point O on the line.
Then, the distance of COM of the whole area from O will be –
\bar {x} = \left ( \frac {a_1 x_1 + a_2 x_2 + ..... }{a_1 + a_2 + ..... } \right )
= \left ( \frac { \sum {a x}}{ \sum {a}} \right )
= \left ( \frac { \sum {a x}}{A} \right ) ………… (3)
From the equations (1), (2) and (3), it is clear that for a body with fixed density or specific gravity, the COM can be determined by the principle of symmetry.
Principle of Symmetry
Principle of symmetry states that –
The distribution of mass or area of a body or surface is equally spaced on both sides of line of symmetry. Therefore centre of mass of a body is located on the line of symmetry.
Therefore, the principle of symmetry can be used to find the centre of mass of geometrically symmetrical objects. Such as –
- COM of a circle or circular lamina.
- Mass centre of a triangle or triangular lamina.
- COM of a parallelogram or a rectangular lamina.
- Mass centre of an uniform diameter rod.
Centre of Mass of Circular Lamina
By the principle of symmetry, the centre of the circle is the centroid of a circular area. Therefore, COM of a circular area lies at the centre of circle.
Centre of Mass of Triangular Lamina
Consider about a triangular lamina ABC in which AD is one of the medians of the triangle \triangle {ABC} .
A triangular lamina \triangle {ABC} is shown in figure. Let, PQ is a thin strip parallel to the base BC . Then PQ is bisected by AD . Hence, centre of mass of PQ will lie on line AD .
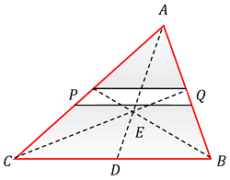
Similarly, the centre of gravity of any other strip parallel to BC will also lies on line AD . Hence, the centre of mass of the whole triangle will lie on line AD .
By similar reasoning we see that, the centre of mass of the triangle will also lies on the other two medians through the vertex B \ \text {and} \ C .
Hence, the COM of the triangle is the point of concurrence of the three medians. This point is called the centroid of the triangle.
IMPORTANT –
Lamina – A lamina is a thin plain two dimensional area having negligible thickness.
Median of Triangle – (1) A line joining one vertex of triangle with mid point of the opposite side of the triangle is called a median. (2) A median divides a triangle into two equal halves of equal area. (3) A triangle has three medians which are concurrent at point E. The point of concurrency is called centroid of the triangle.
Centre of Mass of Parallelogram
Consider about a parallelogram ABCD and let its two diagonals AC \ \text {and} \ BD intersect at point E .
Since, the diagonals of a parallelogram bisect to each other, so E will be the middle point of diagonals AC \ \text {and} \ BD both as shown in figure.
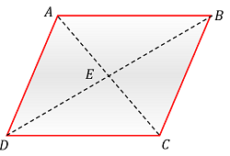
Consider about the diagonal AC which divides the parallelogram into two equal triangles \triangle {ABC} and \triangle {ADC} .
Then, by the discussion of centre of mass of a triangle, we have –
- COM of triangle \triangle {ABC} will lie on line BE .
- COM of triangle \triangle {ADC} will lie on line DE .
Hence, the COM of the parallelogram ABCD will lie on diagonal BD .
In similar manner, considering about the diagonal BD , we can see that COM of parallelogram will lie on diagonal AC .
Therefore, the centre of gravity of parallelogram is at the common point on diagonals AC and BD which is the point of intersection of diagonals i.e. the point E .
Centre of Mass of Uniform Rod
By the principle of symmetry, it is clear that the centre of mass of a uniform diameter rod lies at the middle point of its axis.
Therefore, the centre of gravity of an uniform rod of length ( l ) lies at position \left ( \frac {l}{2} \right ) from one end of the rod.
Centre of Mass of Simple Shapes
COM of simple geometrical shapes and having homogeneous density are located at its geometrical centroids.
Example –
- For a rectangle, square or parallelogram shaped objects, COM is located at the point of intersection of their two diagonals.
- For equilateral triangular shape object, COM is located at intersection point of perpendicular bisectors of three sides. ( For an equilateral triangle, intersection point of perpendicular bisectors of three sides and intersection point of three medians lie at same point. )
- For circular disc or concentric annular ring shaped objects, COM is located at the centre of circles.
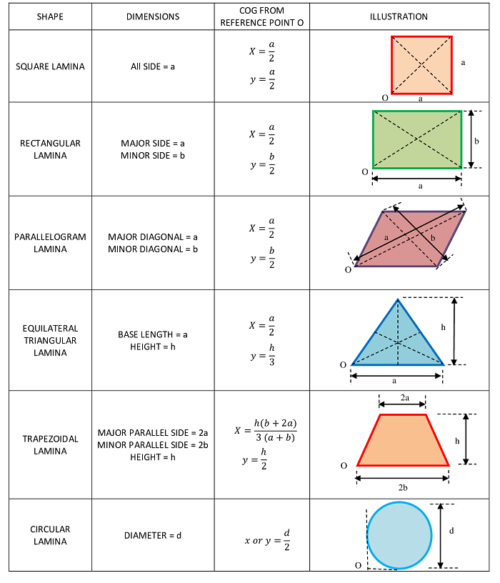
Centroid of simple geometrical shapes is provided in a tabular form below –
See numerical problems based on this article.
