“Heat Energy” Numerical Problems
Try to solve the following “Heat Energy” numerical problems to clear the concepts in solving the numerical problems.
First of all go to the theory portion of the respective topic and then try to solve the numerical problems by yourself. If facing problem in solving the numerical, click on the Go to solution button to see the ready made solution placed at the bottom of each numerical problem.
01) PROBLEM – P050101
A blacksmith fixes iron rings on the rim of wooden wheels of a bullock cart. The diameters of the wheel and the iron ring are ( 5.243 \ m ) and ( 5.231 \ m ) respectively at 27 \degree C . To what temperature should the ring be heated so as to fit the rim of the wheel? Given for iron coefficient of linear expansion ( \alpha = 1.2 \times 10^{-5} \degree C^{-1} ) .
Keywords related to this problem.
02) PROBLEM – P050102
A clock with iron pendulum keeps correct time at 20 \degree C . How much will it loose or gain if temperature changes to 40 \degree C ? Coefficient of cubical expansion of iron is ( \gamma = 36 \times 10^{-5} \degree C^{-1} )
Keywords related to this problem.
03) PROBLEM – P050103
What should be the lengths of steel and copper rods at 0 \degree C so that the length of steel rod is ( 5 \ cm ) longer than copper at all temperatures? Given ( \alpha_{steel} = 1.1 \times 10^{-5} \degree C^{-1} ) and ( \alpha_{copper} = 1.7 \times 10^{-5} \degree C^{-1} )
Keywords related to this problem.
04) PROBLEM – P050104
A one liter flask contains some mercury. It is found that at different temperatures, the volume of air inside the flask remains the same. What is the volume of mercury in this flask? Given, for glass ( \alpha = 9 \times 10^{-6} \degree C^{-1} ) and for mercury ( \gamma = 36 \times 10^{-6} \degree C^{-1} )
Keywords related to this problem.
05) PROBLEM – P050105
An ice cube of mass ( 0.1 \ kg ) at 0 \degree C is placed in an isolated container which is at 227 \degree C . The specific heat S of the container varies with temperature T according to the empirical relation ( S = A + BT ) . Where \left ( A = 100 \ cal / kg \ K \right ) and \left ( B = 2 \times 10^{-2} \ cal / kg \ K^2 \right ) . If the final temperature of the container is 27 \degree C , determine the mass of the container.
Latent heat of fusion of water ( L = 8 \times 10^4 \ cal / kg ) and specific heat of water ( C = 10^3 \ cal / kg \ K )
Keywords related to this problem.
06) PROBLEM – P050106
A sphere of diameter ( 7 \ cm ) and mass ( 266.5 \ g ) floats in a bath of a liquid. As the temperature is raised, the sphere just begins to sink at a temperature of 35 \degree C . If the density of liquid at 0 \degree C is ( 1.527 \ g \ cm^{-3} ) , find the coefficient of cubical expansion of the liquid. Neglect the expansion of the sphere.
Keywords related to this problem.
07) PROBLEM – P050107
A bimetallic strip is formed out of two identical strips, one of copper and the other of brass. The coefficients of linear expansion of the two metals are ( \alpha_{C} ) and ( \alpha_{B} ) . On heating, the temperature of the strip goes up by ( \Delta T ) and the strip bends to form an arc of radius of curvature ( R ) . Then find a relation between ( \Delta T ), \ ( \alpha_{C} ), \ ( \alpha_{B} ) \ \& \ ( R ) .
Keywords related to this problem.
08) PROBLEM – P050108
Three rods made up of the same material and having the same cross section have joined as shown in figure. Each rod is of the same length. The left and right ends are kept at 0 \degree C and 90 \degree C respectively. What will be the temperature of the junction?
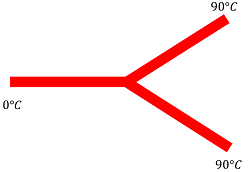
Keywords related to this problem.
09) PROBLEM – P050109
Three bars of equal lengths and equal cross sectional area are connected in series. Their thermal conductivity are in the ratio 2 : 4 : 3 . If the open ends of the first and last bars are kept at temperatures of 200 \degree C and 18 \degree C respectively, in the steady state calculate the temperatures of junctions.
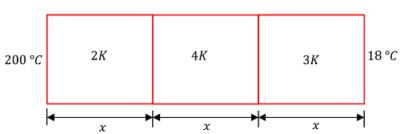
Keywords related to this problem.
10) PROBLEM – P050110
A layer of ice of ( 2 \ cm ) thick is formed on a pond. The temperature of air is ( - 20 \degree C ) . Calculate how long it will take for the thickness of ice to increase by ( 1 \ mm ) . Density of ice ( \rho = 1 \ gm \ cm^{-3} ) . Latent heat of ice ( L = 80 \ cal \ gm^{-1} ) . Conductivity of ice ( K = 0.008 \ cal \ s^{-1} \ cm^{-1} \degree C^{-1} )
Keywords related to this problem.
11) PROBLEM – P050111
A spherical body with radius ( 12 \ cm ) radiates ( 450 \ W ) power at 500 \degree K . If the radius is halved and the temperature is doubled, what would be the power radiated?
Keywords related to this problem.
12) PROBLEM – P050112
Hot oil is circulated through an insulated container with a wooden lid at the top whose conductivity ( K = 0.149 \ J \ m^{-1} \ C^{-1} \ s^{-1} ) , thickness ( t = 5 \ mm ) , emissivity ( \epsilon = 0.6 ) , temperature of top of the lid is maintained at ( T_1 = 127 \degree C ) .
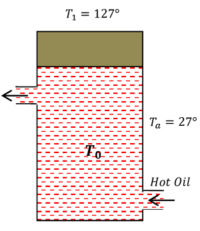
If the ambient temperature ( T_a = 27 \degree C ) (a) Calculate rate of heat loss per unit area due to radiation from the lid. (b) Find the temperature of the oil. Given ( \sigma = \frac {17}{3} \times 10^{- 8} )
Keywords related to this problem.
13) PROBLEM – P050113
A black body initially at 27 \degree C is heated to 327 \degree C . How many times its total heat emitted at the higher temperature than that at lower temperature?
What is the wavelength of the maximum energy radiation at the higher temperature? Wien’s constant is ( 2.898 \times 10^{-3} ) .
Keywords related to this problem.
14) PROBLEM – P050114
Three identical rods A, \ B \ \& C of equal lengths and equal diameters are joined in series as shown in figure. Their thermal conductivity are ( 2K ), \ ( K ) and \left ( \frac {K}{2} \right ) respectively.

Calculate the temperature at two junctions.
Keywords related to this problem.
15) PROBLEM – P050115
One mole of an ideal gas undergoes a cyclic process ABCD where the ( P, \ V ) co-ordinates are A \ (5, 1), \ B \ (5, 3), \ C \ (2, 3) and D \ (2, 1) . Pressure is in atmospheric pressure and Volume is in litre. Calculate work done along AB, \ BC, \ CD \ \& \ DA and also net work done in the process.
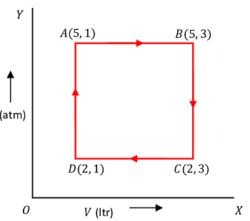
Given, atmospheric pressure ( 1 \ atm = 1.01 \times 10^{-5} \ N \ m^{-2} ) .
Keywords related to this problem.
16) PROBLEM – P050116
A metal of mass ( 1 \ kg ) at constant atmospheric pressure and at initial temperature 20 \degree C is given a heat of ( 20000 \ J ) . Find (i) change in temperature (ii) work done and (iii) change in internal energy.
Given specific heat ( c = 400 \ J \ kg^{-1} \ C^{-1} ) , Coefficient of cubical expansion ( \gamma = 9 \times 10^{-5} \degree C^{-1} ) , Density ( \rho = 9000 \ kg \ m^{-3} ) , Atmospheric pressure ( P = 1 \times 10^{5} \ N \ m^{-2} ) .
Keywords related to this problem.
17) PROBLEM – P050117
A reversible engine converts one fifth of heat which it absorbs from a source into work. When the temperature of the sink is reduced by 70 \degree , its efficiency is doubled. Calculate the temperature of the source and the sink.
Keywords related to this problem.
18) PROBLEM – P050118
A mono-atomic gas of two moles is taken through a cyclic process starting from A as shown in figure.
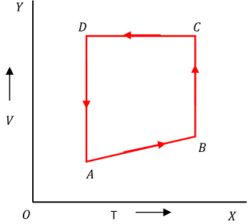
The volume ratios are \left [ \left ( \frac {V_B}{V_A} \right ) = 2 \right ] and \left [ \left ( \frac {V_D}{V_A} \right ) = 4 \right ] . If the temperature T_A at A is 27 \degree C , Calculate (a) the temperature of the gas at point B . (b) heat absorbed or released by the gas in each process (c) the total work done by the gas during complete cycle.
Keywords related to this problem.
19) PROBLEM – P050119
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature. Find the ratio of \left [ \gamma = \left ( \frac {C_p}{C_v} \right ) \right ] for the gas.
Keywords related to this problem.
20) PROBLEM – P050120
A balloon partially filled with Helium gas has a volume of ( 30 \ m^3 ) , at the earth’s surface where pressure is ( 76 \ cm ) of Hg and temperature is 27 \degree C . What will be the increase in volume of the gas if balloon rises to a height where pressure is ( 7.6 \ cm ) of Hg and temperature is ( - 54 \degree C ) ?
Keywords related to this problem.
21) PROBLEM – P050121
A closed container of volume ( 0.02 \ m^3 ) contains a mixture of neon and argon gases at 27 \degree C temperature and ( 1.0 \ \times 10^5 \ N \ m^{-2} ) pressure. If the gram molecular weights of neon and argon are 20 and 40 respectively, find the masses of the individual gases in the container, assuming them to be ideal.
Given ( R = 8.314 \ J \ mole^{-1} K^{-1} ) . Total mass of the mixture is ( 28 \ g ) .
Keywords related to this problem.
22) PROBLEM – P050122
Two thermally insulated vessels 1 and 2 are filled with air at temperature ( T_1 \ \& \ T_2 ) and volumes ( V_1 \ \& \ V_2 ) and pressure ( P_1 \ \& \ P_2 ) respectively. If the valve joining the two vessels is opened, what will be the temperature inside the vessel at equilibrium?
Keywords related to this problem.
23) PROBLEM – P050123
A gaseous mixture enclosed in a vessel contains ( 1 ) gram mole of a gas A with \left ( \gamma = \frac {5}{3} \right ) and another gas B with \left ( \gamma = \frac {7}{5} \right ) at a temperature T . The gases A and B do not react with each other and assumed to be ideal. Find the number of gram moles of B if ( \gamma ) for the gaseous mixture is \left ( \frac {19}{13} \right ) .
Keywords related to this problem.
24) PROBLEM – P050124
A thin tube sealed at both ends is ( 100 \ cm ) long. It lies horizontally, the middle ( 10 \ cm ) containing mercury and the two equal ends containing air at standard atmospheric pressure. If the tube is now turned to a vertical position, by what will the mercury be displaced?
Keywords related to this problem.
25) PROBLEM – P050125
A thin tube of uniform cross section is sealed from both ends. When it lies horizontally the middle ( 5 \ cm ) length contains mercury and the two ends contain air at the same pressure P . When the tube is held at an angle of 60 \degree with the vertical, then the lengths of the air columns above and below the mercury column are ( 46 \ cm ) and ( 44.5 \ cm ) respectively. Calculate the pressure P in cm of mercury. The temperature of the system is kept at 30 \degree C .
Keywords related to this problem.
