Bernoulli’s Theorem

What is Bernoulli’s theorem?

Bernoulli’s theorem states that –

“Total energy of a liquid particle in a perfect in-compressible liquid flowing in a continuous stream in a pipe remains constant.”

• Bernoulli’s theorem is associated with the energy of a flowing fluid.
• Bernoulli’s theorem statement is based on the assumption that, there are no energy loss due to friction in the pipe.

Therefore, according to the Bernoulli’s statement –

\quad \left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) = \text {Constant} .

Or, \quad \text {Total energy of liquid} = \text {Potential energy} \ ( Z ) + \text {Pressure energy} \left ( \frac {p}{w} \right ) + \text {Kinetic energy} \left ( \frac {v^2}{2 g} \right ) = \text {Constant} .

Energy of a fluid

Energy of a fluid body is defined as its capacity of doing work.

A fluid body can possess various forms of energies of which the following types of energies are most important.

1. Potential energy.
2. Pressure energy.
3. Kinetic energy.

Potential energy

Potential energy is the energy possessed by a fluid body by virtue of its position or location in space.

Consider about ( W ) kg of a fluid kept at a height of ( Z ) meters above a datum line. The potential energy of that fluid will be equal to ( WZ ) \ \text {kg-m}

Thus, the potential energy per kg of the fluid body will be –

\left ( \frac {W Z}{W} \right ) \left ( \frac {\text {kg-m}}{\text {kg}} \right ) = Z \ \text {mtr.} .

• We can say that, pressure head due to potential energy of the fluid is ( Z ) \ \text {mtr.}

Pressure energy

Pressure energy is the energy possessed by a fluid by virtue of the pressure at which it is maintained.

Consider that, ( W ) kg of a fluid body is under a pressure of ( p ) \ \text {kg-m}^{-2} . Then the pressure energy of the fluid will be –

W \left ( \frac {p}{w} \right ) \ \text {kg} \left ( \frac {\text {kg-m}^{-2}}{\text {kg-m}^{-3}} \right ) = W \left ( \frac {p}{w} \right ) \ \text {kg-m}

Where ( w ) is the specific weight of the fluid in \text {kg-m}^{-3} .

Therefore, pressure head per kg of the fluid under pressure will be \left ( \frac {p}{w} \right ) \ \text {mtr.}

• We can say that, pressure head due to pressure energy of the fluid is \left ( \frac {p}{w} \right ) \ \text {mtr.}

Kinetic energy

Kinetic energy is the energy possessed by a fluid body by virtue of its motion.

Consider that, ( W ) kg of a fluid is moving at a velocity of ( v ) \text {m-s}^{-1} .

Then, the kinetic energy of fluid will be –

W \left ( \frac {v^2}{2 g} \right ) \ \text {kg-m}

Therefore, kinetic energy per kg of the fluid body will be –

\left ( \frac {v^2}{2 g} \right ) \ \text {mtr.}

• We can say that, pressure head due to kinetic energy of the fluid is \left ( \frac {v^2}{2 g} \right ) \ \text {mtr.}

Total energy

If a fluid body of weight ( W ) \ \text {kg} is at a height of ( Z ) \ \text {mtr.} above a datum line, and at a pressure intensity of ( p ) \ \text {kg-m}^{-2} and moving with a velocity of ( v ) \ \text {m-s}^{-1} , then the total energy of the fluid body will be –

W \left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) \ \text {kg-m}

Therefore, total energy per kg of the fluid body will be –

\left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) \ \text {mtr.}

• We can say that, the pressure head due to total energy is –

\left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) \ \text {mtr.}

• It is also known as total energy head.

Equation of cotinuity

Consider about a perfect in-compressible liquid flowing through a non-uniform pipeline as shown in figure. In this, consider about two sections AA \text {and} BB of the pipe. Assume that, the pipe is running full and there is a continuity of flow between the two sections.

Let –

• ( Z_1 ) is height of section AA above the datum line.
• ( p_1 ) is pressure of fluid at section AA .
• ( v_1 ) is velocity of liquid at section AA .
• ( a_1 ) is area of cross section of the pipe at section AA .

And Z_2, \ p_2, \ v_2, \ a_2 are the corresponding values at section BB .

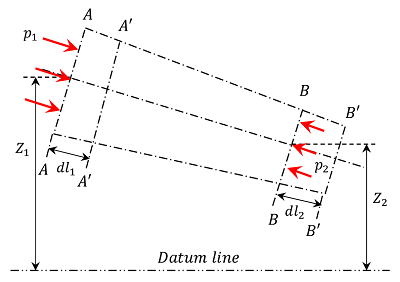
Let, the liquid between the two sections AA \ \text {and} \ BB move to sections A'A' \ \text {and} \ B'B' .

Let, the length of pipe between the sections AA \ \text {and} \ A'A' is ( dl_1 ) and between sections BB \ \text {and} \ B'B' is ( dl_2 ) as shown in figure.

This movement of liquid between AA \ \text {and} \ BB is equivalent to the movement of the liquid particles between AA \ \text {and} \ A'A' \ \text {to} \ BB \ \text {and} \ B'B' , the remaining liquid between sections A'A' \ \text {and} \ BB remains unaffected.

Let, ( W ) is the weight of the liquid between AA \ \text {and} \ A'A' .

We can apply Bernoulli’s theorem in the flow of liquid between the sections AA \ \text {and} \ BB

• Since the flow is continuous, therefore –

W = w \ a_1 \ dl_1 = w \ a_2 \ dl_2

Or, \quad a_1 \ dl_1 = \frac {W}{w} \quad \text {and} \quad a_2 \ dl_2 = \frac {W}{w}

Therefore, \quad a_1 \ dl_1 = a_2 \ dl_2

Expression for Bernoulli’s equation

• Work done by the pressure ( p_1 ) at AA , in moving the liquid from AA \ \text {to} \ A'A' is –

\text {Force} \times \text {Distance} = ( p_1 \ a_1 ) \times dl_1

• Similarly, work done by pressure at BB in moving the liquid from BB \ \text {to} \ B'B' is –

\text {Force} \times \text {Distance} = - ( p_2 \ a_2 ) \times dl_2

Minus sign is taken as the direction of ( p_2 ) is opposite to that of ( p_1 ) .

• Total work done by the fluid pressure will be –

( p_1 \ a_1 ) dl_1 - ( p_2 \ a_2 ) dl_2

Or, \quad p_1 \ a_1 \ dl_1 - p_2 \ a_2 \ dl_2

By substituting \quad ( a_2 \ dl_2 ) = ( a_1 \ dl_1 ) , we get –

• Work done by the fluid pressure is –

p_1 \ a_1 \ dl_1 - p_2 \ a_1 \ dl_1 = a_1 \ dl_1 ( p_1 - p_2 )

= \frac {W}{w} ( p_1 - p_2 )

• Loss of potential energy in moving the fluid from AA \ \text {to} \ BB is –

W ( Z_1 - Z_2 )

• And gain in kinetic energy in moving the fluid from AA \ \text {to} \ BB is –

W \left ( \frac {v_2^2}{2g} - \frac {v_1^2}{2g} \right ) = \frac {W}{2g} \left ( v_2^2 - v_1^2 \right )

By principle of conservation of energy, we know that –

\text {Loss of potential energy} + \text {Work done by pressure} = \text {Gain in kinetic energy}

Therefore, \quad W ( Z_1 - Z_2 ) + \frac {W}{w} ( p_1 - p_2 ) = \frac {W}{2g} ( v_2^2 - v_1^2 )

Or, \quad ( Z_1 - Z_2 ) + \frac {p_1}{w} - \frac {p_2}{w} = \frac {v_2^2}{2g} - \frac {v_1^2}{2g}

Or, \quad Z_1 + \frac {p_1}{w} + \frac {v_1^2}{2g} = Z_2 + \frac {p_2}{w} + \frac {v_2^2}{2g}

• This expression is generally called as Bernoulli’s equation.