What is called a “Uniform Circular Motion”?
Curvilinear motion is the motion of an object along the circumference of a circular path or a curve of any shape or rotation of an object along a circular path. A curvilinear motion can be of following types –
- Curve motion – A motion along the curvature of a curved path. Example – Motion of a car while taking a turn on curved road.
- Projectile motion – A motion under the influence of gravity along the parabolic curvature. Example – Trajectory of motion of a javelin thrown in ground.
- Circular motion – A motion along the circumference of a circular path. Example – Running of an athlete around a circular ground.
- Rotary motion – A motion in which a body rotates about its own axis. Example – Rotation of earth about its own axis.
Circular Motion
If a particle moves along a circular path, then it’s motion is called a circular motion. A circular motion is of two types –
- Non-uniform circular motion – It is the motion of a body moving along a circular path with varying angular acceleration.
- Uniform circular motion – It is the motion of a body moving along a circular path with constant angular acceleration.
Therefore, if a particle moves along a circular path with a constant speed i.e. it covers equal distances along the circumference of the circle in equal intervals of time, then it’s motion is called a uniform circular motion.
A uniform circular motion is an accelerated motion and concerned acceleration is known as centripetal acceleration.
Most important terms related to a uniform circular motion are –
- Angular Displacement.
- Angular velocity.
- Angular acceleration.
- Time period.
- Frequency.
1. Angular Displacement
Consider about a particle moving in a circular path as shown in figure. Let, the particle is initially at point A and after time ( t ) it reaches at the point P .
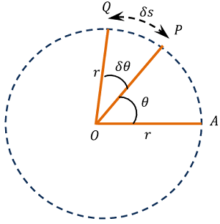
Let, \quad \angle {AOP} = \theta
Now let, Q is the position of the particle after further time ( \delta t ) .
Let, \quad \angle {POQ} = \delta \theta
Then ( \delta \theta ) is called angular displacement of the particle in time ( \delta t ) . It is measured in radians.
2. Angular Velocity
The rate of change of subtended angle ( \theta ) at centre O is called angular velocity of the particle.
From figure, in time ( \delta t ) , the average angular velocity of particle is given by –
\bar {\omega} = \frac {\text {Angular Displacement}}{\text {Time}} = \left ( \frac {\delta \theta}{\delta t} \right )
Therefore, angular velocity of the particle at point P will be –
\omega = \lim\limits_{Q \rightarrow P} \left ( \frac {\delta \theta}{\delta t} \right ) = \left ( \frac {d \theta}{dt} \right )
Therefore, angular velocity ( \omega ) of a particle is the first order derivative of angular displacement ( \theta ) with respect to time.
3. Angular Acceleration
The rate of change of angular velocity is called angular acceleration.
Therefore, Angular acceleration = Rate of change of angular velocity.
Or, \quad \alpha = \left ( \frac {d \omega}{d t} \right ) = \frac {d}{d t} \left ( \omega \right )
Therefore, angular acceleration ( \alpha ) of a particle is the first order derivative of angular velocity ( \omega ) with respect to time.
Again \quad \omega = \left ( \frac {d \theta}{d t} \right )
Therefore, \quad \alpha = \frac {d}{dt} \left ( \frac {d \theta}{dt} \right ) = \left ( \frac {d^2 \theta}{d t^2} \right )
Therefore, angular acceleration ( \alpha ) of a particle is the second order derivative of angular displacement ( \theta ) with respect to time.
Again, \quad \left ( \frac {d \omega}{d t} \right ) = \left ( \frac {d \omega}{d \theta} \right ) \times \left ( \frac {d \theta}{d t} \right ) = \left ( \frac {d \omega}{d \theta} \right ) \omega
Or, \quad \alpha = \omega \left ( \frac {d \omega}{d \theta} \right )
Therefore, angular acceleration ( \alpha ) of a particle is the first order derivative of angular velocity ( \omega ) with respect to angular displacement ( \theta ) .
4. Time period
Time taken by a particle to complete one complete revolution along its circular path is called its period of revolution or Time period.
If time period is denoted by ( T ) , then angular displacement ( \theta ) in time ( T ) will be ( 2 \pi ) radians.
5. Frequency of motion
Number of revolutions per unit time is called frequency.
Therefore, frequency of revolutions is given by –
\nu = \left ( \frac {1}{T} \right )
But, \quad \text {Angular velocity} = \text {Angular displacement per unit time}
We know that, total displacement in one complete revolution is ( \theta = 2 \pi ) radians.
Therefore, \quad \omega = \left ( \frac {\theta}{t} \right ) = \left ( \frac {2 \pi}{T} \right )
= 2 \pi \left ( \frac {1}{T} \right ) = 2 \pi \nu
Where, ( \nu ) is the frequency of revolutions.
Or, \quad \omega = 2 \pi \nu
Relation between Linear & Angular quantities
Very simple relation exist between linear quantities and angular quantities of motion. These are as follows –
Linear Displacement & Angular Displacement
From figure, in time ( \delta t ) , linear linear displacement of the particle will be ( PQ = ds ) .
We know that, \quad \text {Arc} = \text {Radius} \ \times \ \text {Angle in radians}
Therefore, linear displacement of the particle is –
\delta s = r \times \delta \theta
Therefore, \quad \text {Linear displacement} = \text {Radius} \ \times \ \text {Angular displacement}
Linear Velocity & Angular Velocity
Consider about a particle revolving in a circular path as shown in figure.
Let, the particle describes a circle of radius, ( r ) with constant linear speed, ( v ) and angular velocity ( \omega ) .
Let, A is the position of particle at any instant and P is the position after one second. Then length of arc ( AP ) is the actual distance traveled in one second which is called linear velocity ( v )
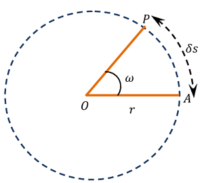
Also angular velocity of particle \quad \angle {AOP} = \omega radians.
But \quad \left ( \frac {\text {Arc AP}}{OA} \right ) = \angle {AOP} in radians.
Now, linear velocity \quad v = \left ( \frac {ds}{dt} \right )
But, \quad ds = ( r \times d \theta )
Therefore, \quad v = \left ( \frac {r \times d \theta}{dt} \right ) = \left ( r \times \omega \right )
Or, \quad v = \omega r
Therefore, \quad \text {Linear velocity} = \text {Radius} \ \times \ \text {Angular velocity}
Linear Acceleration & Angular Acceleration
We know that, \quad v = \omega r
Differentiating this equation with respect to time, we will get –
\left ( \frac {dv}{dt} \right ) = r \left ( \frac {d \omega}{dt} \right )
But, \quad \left ( \frac {dv}{dt} \right ) = a \quad and \quad \left ( \frac {d \omega}{dt} \right ) = \alpha
Therefore, \quad a = r \alpha
Therefore, \quad \text {Linear acceleration} = \text {Radius} \ \times \ \text {Angular acceleration}
Planer or Curvilinear Motion
Out of three coordinates, if two co-ordinates are required to specify the position of a moving object, then the motion of the object is called a curvilinear motion.
It is a two dimensional motion which is commonly known as a planer motion.
Examples –
- Motion of planets around the sun.
- A car moving in a curved path.
- Circular motion etc.
See numerical problems based on this article.
