Kepler’s Law

What are Kepler’s Laws of Planetary motion?

To explain the motion of planets, Kepler formulated three laws which are popularly known as Kepler’s law of planetary motion. These are –

1. First law of Elliptical orbits (Law of Ellipses).
2. Second law of areas (Law of Equal Areas).
3. Third law of periods (Law of Harmonies).

Kepler’s First Law of Elliptical Orbit

Kepler’s law states that, each planet revolves around the sun in an elliptical orbit with the sun situated at one of the two foci.

• This law is also called as Kepler’s law of elliptical orbits.
• Planets move around the sun in elliptical orbits as shown in figure.

An ellipse has two foci S and S' . The sun remains located at one focus S .

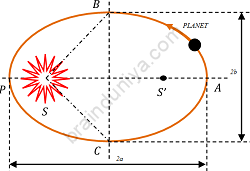
The points P and A  on the orbit are called the perihelion and the aphelion which represents the closest and farthest distances from the sun respectively.

Kepler’s Second Law of Areas

Kepler’s law states that, the radius vector drawn from the sun to a planet sweeps out equal areas in equal intervals of time.

• This means that, the areal velocity ( area covered per unit time ) of a planet around the sun is constant.

Consider about a planet moving in an elliptical orbit as shown in figure.

• Suppose time taken by planet to move from A to B  is same as time taken to move from C  to D .
• From Kepler’s second law, the swept area ASB and CSD  covered in equal time must be equal.
• Clearly, the planet covers a larger distance CD  when it is near the sun than AB  when it is farther away in the same interval of time.

  

• Hence, the linear velocity of a planet is more when it is closer to the sun.

Kepler’s Third Law of Period

Kepler’s law states that, the square of the period of revolution of a planet around the sun is proportional to the cube of the semi-major axis of its elliptical orbit.

Consider about the figure as shown above.

• Major axis of the elliptical orbit is ( 2a ) .
• Therefore, semi-major axis will be ( a ) .

If ( T ) is the period of revolution of a planet, then –

T^2 \propto a^3

Or, \quad T^2 = K a^3 where K is a constant of proportionality.

Satellite

A satellite is a small body which continuously revolves by its own around a much larger body in a stable orbit due to effect of gravitational force of attraction.

Based upon their origin and type of motion, satellites are of following three types –

1. Natural satellite.
2. Artificial satellite.
3. Geostationary satellite.

Natural Satellite

A satellite created by nature itself is called a natural satellite.

Earth is regarded as a natural satellite of Sun and Moon is a natural satellite of the earth itself.

Artificial Satellite

A satellite made by human is called an artificial satellite.

The first artificial satellite is SPUTNIK-I made by Russia in 1957 . After that many artificial satellites have been put into orbits around the earth to study various phenomenon in the outer regions of the earth’s atmosphere.

To put a satellite into an orbit around the earth, we need to give it two velocities –

1. A minimum vertical velocity called escape velocity, to take the satellite to a suitable height.
2. After the satellite has ascended the required height, it is given a suitable horizontal velocity to make it to move in circular orbit around the earth.

Geostationary Satellite

If a satellite is made to revolve around earth from West to East with a period of revolution of 24 hours in a circular orbit concentric and co-planar with the equatorial plane of the earth, its relative velocity with respect to the earth will be zero.

Such a satellite is called geostationary satellite because it appears stationary to an observer on the earth.

Escape Velocity

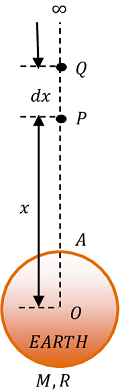
Escape velocity is the minimum velocity by which a body must be projected vertically upwards so that it may just escape beyond the effect of gravitational field of earth.

Consider about a body of mass ( m ) lies at point P  at a distance ( x )  from its centre as shown in figure.

• The gravitational force of attraction on the body at point P  is –

F = \left ( \frac { G M m }{ x^2 } \right )

• The small work done in moving the body through a small distance ( PQ = dx ) against the gravitational force is given by –

d W = F dx = \left ( \frac { G M m }{ x^2 } \right ) dx

• The total work done in moving the body from surface of the earth to a region beyond the gravitational field of the earth i.e. work done in moving the body from \left ( x = R \right ) to \left ( x = \infty \right )  will be –

W = \int {d W} = \int\limits_{ R }^{ \infty } \left ( \frac { G M m }{ x^2 } \right ) dx = ( G M m ) \int\limits_{ R }^{ \infty } x^{ -2 } dx

Or, \quad W = ( G M m ) \left [ - \frac { 1 }{ x } \right ]_{ R }^{ \infty } = ( G M m ) \left ( - \frac { 1 }{ \infty } + \frac { 1 }{ R } \right ) = \left ( \frac { G M m }{ R } \right )

Or, \quad W = \left ( \frac { G M m }{ R } \right )

If ( v_e ) is the escape velocity of the body, then the kinetic energy imparted to the body must be just sufficient to perform the work ( W ) .

• Therefore, \quad \left ( \frac { 1 }{ 2 } \right ) m v_e^2 = \left ( \frac { G M m }{ R } \right )

Or, \quad v_e^2 = \left ( \frac { 2 G M }{ R } \right )

• Hence, escape velocity \quad v_e = \left ( \sqrt \frac { 2 G M }{ R } \right ) …….. (1)

But, \quad g = \left ( \frac { G M }{ R^2 } \right ) \quad Putting this value in equation (1)

• Therefore, \quad v_e = \sqrt { \left ( 2 g R \right ) } ……… (2)

Orbital Velocity

Orbital velocity is defined as the required velocity to put a satellite into its orbit around the earth.

Let –

• ( M ) is the mass of the earth.
• ( R ) is the radius of the earth.
• ( m ) is the mass of satellite.
• ( v_0 ) is the orbital velocity of the satellite.
• ( h ) is the height of satellite above the earth’s surface.

According to laws of gravitation, the force of gravity on the satellite is –

F = \left [ \frac { G M m }{ \left ( R + h \right )^2 } \right ] .

This gravitational force provides necessary centripetal force to the satellite to keep it in its orbit.

• Centripetal force on a body is given by –

F = \left [ \frac { m v_0^2 }{ \left ( R + h \right ) } \right ]

Therefore, \left [ \frac { m v_0^2 }{ \left ( R + h \right ) } \right ] = \left [ \frac { G M m }{ \left ( R + h \right )^2 } \right ]

Or, \quad v_0^2 = \left [ \frac { G M }{ \left ( R + h \right ) } \right ]

• Therefore, orbital velocity \quad v_0 = \sqrt { \frac { G M }{ \left ( R + h \right ) }} ……….. (1)

If ( g )  is the acceleration due to gravity on the earth’s surface, then –

g = \left ( \frac { G M }{ R^2 } \right )

Or, \quad G M = g R^2

Putting this in equation (1), we have –

v_0 = \sqrt { \frac { g R^2 }{ ( R + h )}} = \sqrt { \frac { g R }{ \left ( 1 + \frac { h }{ R } \right ) }}

When, satellite is close to the earth’s surface, \left ( h << R \right ) .

• Therefore, \quad \left ( \frac { h }{ R } \right ) = 0

Or, \quad v_0 = \sqrt { g R }

From equation (1), it is clear that –

1. Orbital velocity is independent of mass of satellite.
2. It decreases with increases in the radius \left ( R + h \right ) .
3. It depends on the mass and radius of the planet about which the satellite revolves.

See numerical problems based on this article.

• P040107
• P040108
• P040109