Degree of Freedom

What is called Degree of Freedom of molecules?

Degree of freedom of a system is defined as the total number of independent ways in which the particles of the system can absorb energy.

In general, the number of degrees of freedom of a system is equal to the total number of the coordinates required to specify the positions of the constituent particles of the system minus the number of independent relations existing between the particles. Let –

• N = number of particles in the system,
• k = number of independent relations between the particles,

Then, the number of degrees of freedom of the system will be –

f = \left ( 3 N - k \right )

Degree of Freedom of Mono-atomic Gas

Gases like He, \ Ne, \ Ar etc. are consists of single atom. These are called mono-atomic gases which have following properties –

• Mono-atomic gases consists of one atom. Hence, independent relation between particles is zero.
• Atoms are capable of translator motion only.

Therefore, for mono-atomic gases –

1. Number of atoms \left ( N = 1 \right )
2. Independent relation between two atoms \left ( k = 0 \right )

So \quad f = \left ( 3 \times 1 - 0 \right ) = 3

Degree of Freedom of Di-atomic Gas

Molecules of gases like N_2, O_2, H_2, CO etc. consists of two atoms. These are called di-atomic gases which have following properties –

• Independent relation between two atoms of a molecule is 1
• Two atoms are at a fixed distance apart.
• The molecule has 3 degrees of freedom corresponding to translator motion and [ ( 3 - 1 ) = 2 ] degrees of freedom corresponding to rotational motion about two mutually perpendicular axes.

Therefore, for di-atomic gas –

1. Number of atoms \left ( N = 2 \right )
2. Independent relation between two atoms \left ( k = 1 \right )

So, \quad f = \left ( 3 \times 2 - 1 \right ) = 5 ( without vibration freedom )

If vibration mode is also possible then –

f = \left ( 5 + 2 \right ) = 7

Degree of Freedom of Tri-atomic Gas

Tri-atomic molecules are of two types –

1) Nonlinear molecules –

In non-linear tri-atomic molecules like H_2 O, S O_2 etc. the three atoms are located at vertices of a triangle. These have following properties –

• Independent relations between atoms of a molecule are 3 .
• These molecule have 3 degrees of freedom corresponding to translator motion.
• These molecules have 3 degrees of freedom corresponding to rotational motion about two mutually perpendicular axes.

Therefore, for non-linear tri-atomic gas –

1. Number of atoms \left ( N = 3 \right )
2. Independent relation between two atoms \left ( k = 3 \right )

So, \quad f = \left ( 3 \times 3 - 3 \right ) = 6

2) Linear molecules –

In linear tri-atomic molecules like C S_2, \ C O_2, \ HCN etc. the three atoms are arranged in a straight line. These have following properties –

• The number of independent relations between atoms of molecules is 2
• These molecule have 3 degrees of freedom corresponding to translator motion.
• These molecules have 3 degrees of freedom corresponding to rotational motion about two mutually perpendicular axes.

Therefore, for linear tri-atomic gas –

1. Number of atoms \left ( N = 3 \right )
2. Independent relation between two atoms \left ( k = 2 \right )

So, \quad f = \left ( 3 \times 3 - 2 \right ) = 7

Law of Equipartition of energy

The law of equipartition of energy states that –

In thermal equilibrium the energy is equally distributed in its various degrees of freedom and the energy associated with each degree of freedom per molecule is \left ( \frac {1}{2} k_B T \right ) where ( k_B ) is the Boltzmann’s constant and ( T ) is the absolute temperature of the system.

Therefore, if a molecule has ( f ) degree of freedom, then energy ( U ) possessed by the molecule will be –

\left [ \left ( \frac {1}{2} \right ) k_B T \right ] \times f

Or, \quad U = \left ( \frac {f}{2} \right ) k_B T

Specific Heat of Poly-atomic Gas

Consider about one mole of a poly-atomic gas at temperature ( T ) . Suppose total degree of freedom of each molecule is ( f ) .

According to law of equipartition of energy the average energy of one molecule is –

U = \left ( \frac {f}{2} \right ) k_B T

Therefore, energy of one mole of gas will be –

U = \left ( \frac {f}{2} \right ) k_B T \times N_A

Where, ( N_A ) is the Avogadro’s number and \left [ k_B = \left ( \frac {R}{N_A} \right ) \right ]

Therefore, \quad U = \left ( \frac {f}{2} \right ) RT ……… (1)

Differentiating equation (1) we get specific heat of gas at constant volume –

C_V = \left ( \frac {dU}{dT} \right ) = \left ( \frac {f}{2} \right ) R ……… (2)

And specific heat of gas at constant pressure –

C_P = ( C_V + R ) = \left ( \frac {f}{2} \right ) R + R

Or, \quad C_P = R \left [ 1 + \left ( \frac {f}{2} \right ) \right ] ………. (3)

Dividing equation (3) by equation (2), we get –

\left ( \frac {C_P}{C_V} \right ) = \left [ \frac { R \left [ 1 + \left ( \frac {f}{2} \right ) \right ] }{ \left ( \frac {f}{2} \right ) R } \right ]

= \left [ \frac { \left ( 1 + \frac {f}{2} \right ) }{\left ( \frac {f}{2} \right ) } \right ]

= \gamma

Therefore, \quad \gamma = \left [ \frac { \left ( 1 + \frac {f}{2} \right ) }{\left ( \frac {f}{2} \right ) } \right ]

= \left [ 1 + \left ( \frac {2}{f} \right ) \right ]

Dulong & Petits Law

Dulong and Petit’s law is related to the specific heat of solid substances. It states that –

At room temperature the molar specific heat of most of solids at constant volume is equal to ( 3 R ) or ( 25 \ \text {J-mol}^{-1} \ K^{-1} ) or ( 6 \ \text {Calorie-mole}^{-1} \ K^{-1} )

In solids, the atoms vibrate about their mean position. During vibrations their energy continuously changes from kinetic energy ( E_k ) to potential energy ( E_p ) and vice versa similar to the energy change in periodic vibrations.

Therefore, in solid object –

1. The average value of ( E_k ) and ( E_p ) are equal.
2. Atoms can vibrate along three mutually perpendicular axes. They have 3 degrees of freedom.

By the law of equipartition of energy, we get for one atom –

E_k = 3 \times \left ( \frac {1}{2} \right ) k_B T = \left ( \frac {3}{2} \right ) k_B T

And \quad E_p = 3 \times \left ( \frac {1}{2} \right ) k_B T = \left ( \frac {3}{2} \right ) k_B T

Therefore, average vibration energy per atom will be –

( E_k + E_p ) = 3 k_B T

The total vibration energy or the internal energy of one mole of atoms of the solid is given by –

U = N_A \times 3 k_B T = 3 RT

Because \quad R = k_B N_A

For solids ( \Delta V ) is negligible, so –

\Delta Q = ( \Delta U + P \Delta V ) = \Delta U

Therefore, \quad C_V = \left ( \frac {\Delta Q}{\Delta T} \right )

= \left ( \frac {\Delta U}{\Delta T} \right ) = 3R

This proves the Dulong and Petit’s law.

Debye Temperature

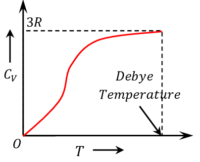
Figure shows the variation of molar specific heat of a solid substance as a function of temperature.

At higher temperature the molar specific heat of all solids is very close to the Dulong and Petit’s value of ( 3 R ) . At lower temperatures the specific heat decreases rapidly due to freezing of some of degrees of freedom. Eventually it becomes zero at ( 0 \degree K ) .

Therefore, vibrational degrees of freedom become active only under certain conditions of temperature.

Debye temperature is the temperature at which the molar specific heat of a solid at constant volume becomes equal to ( 3 R ) , where ( R ) is the universal gas constant.