What is Magnetic Dipole Moment?
Magnetic dipole moment is defined as the product of pole strength of one of the poles of a magnet and magnetic length ( distance between magnetic poles ).
Let, the magnetic length or distance between two poles of a magnetic dipole is ( 2l ) . Let, ( q_m ) is the pole strength of each pole of a bar magnet.
Then magnetic dipole moment is given by –
m = ( q_m \times 2l ) .
Example –
Magnetic needle, bar magnet, current carrying solenoid, a current loop, atoms etc. are examples of magnetic dipoles.
Magnetic Length
Poles of a bar magnet are not situated at the ends. Hence, the exact distance between the poles and the distance between the ends of magnet are not the same.
Original length of a bar magnet is called geometrical length and the distance between the poles is called magnetic length.
Geometrical length is found more than the magnetic length or effective length of a magnet. It is normally ( 0.84 ) times of the geometrical length.
Therefore, \quad \left [ \frac {\text {Magnetic length}}{\text {Geometrical length}} \right ] \cong 0.84
Direction of Magnetic Dipole Moment
Magnetic dipole moment ( m ) is a vector quantity. Its direction is taken in the direction of length taken between the poles.
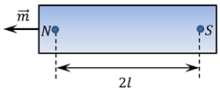
In above figure, the dipole moment at N pole of the magnet will be in the direction leftward i.e. from South pole to North pole because direction of magnetic length is from S to N .
SI unit of dipole moment is \text {Ampere-meter}^2 \ \text {or} \ \text {Joule-Tesla}^{-1}
Pole Strength & Area of Poles
Pole strength of a magnet depends on the cross sectional are of poles.
If a bar magnet is axially cut into two equal halves along the length –
When a bar magnet is axially cut into two equal halves along the length, then the pole strength of each pole reduces to half of its initial value but magnetic length remains the same. Therefore, dipole moment becomes half of original value.
If a bar magnet is cut into two equal halves along perpendicular to the magnetic length –
When a bar magnet is axially cut into equal halves along perpendicular to the magnetic length, then the pole strength of each pole remains the same but magnetic length reduces to half of its initial value. Therefore, dipole moment becomes half of original value.
Torque on Magnetic Dipole
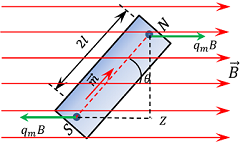
Consider about a magnetic dipole i.e. a bar magnet which is placed in a uniform magnetic field as shown in figure.
Let –
- Magnetic length of magnet is ( 2l )
- Pole strength of each pole is ( q_m )
- Strength of magnetic field is ( B )
- Angle between magnetic dipole moment is ( m ) and magnetic field ( B ) is ( \theta )
Then, force acting on North pole will be –
F_N = q_m \ B \quad This force is acting along the direction of ( \vec {B} ) .
Similarly, force acting on South pole will be –
F_S = q_m \ B \quad This force is acting opposite to the direction of ( \vec {B} ) .
These two equal and opposite forces will constitute a couple which tends to rotate the magnet in clockwise direction. Thus the bar magnet will experiences a torque.
Therefore, torque acting on the bar magnet is given by –
\text {Torque} = \text {Magnitude of one force} \ \times \ \text {perpendicular distance between forces}
Therefore, \quad \tau = F_N \times ZN
= F_S \times ZN
Therefore, \quad \tau = q_m \ B \times ZN
= q_m B ( SN \sin \theta )
= q_m B \left ( 2 l \sin \theta \right )
= ( q_m \times 2 l ) B \sin \theta
= m B \sin \theta
Therefore, \quad \tau = m B \sin \theta
Hence, torque = Magnetic dipole moment × Component of magnetic field perpendicular to dipole moment.
When, ( B = 1 ) unit and ( \theta = 90 \degree )
Then, \quad \tau = m
Therefore, magnetic dipole moment may also be defined as the torque acting on a magnetic dipole placed normal to a uniform magnetic field of unit strength.
See numerical problems based on this article.
