What is Maximum Efficiency of a Machine?
Maximum efficiency of a machine is defined as the ratio of output work and minimum input work required for the work by the machine.
Therefore, maximum efficiency is given by –
\eta = \left ( \frac{\text {Output work}}{\text {Minimum input work}} \right )
So, Maximum Efficiency of a machine will be achieved, when output work will be maximum or Input work will be minimum.
Efficiency of a machine is also defined as the ratio of mechanical advantage obtained from the machine and velocity ratio of the machine.
Therefore, efficiency is given by –
\eta = \left ( \frac{\text {Mechanical advantage}}{\text {Velocity ratio}} \right )
= \left ( \frac{\text {MA}}{\text {VR}} \right )
So, Maximum Efficiency of a machine will be achieved, when Mechanical advantage will be maximum or Velocity ratio will be minimum.
Here, we will discuss about the possibilities of achieving maximum efficiency from a machine.
Mechanical Advantage
Mechanical advantage of a machine is defined as the ratio of load lifted at output end to the effort applied at the input end of the machine.
Therefore, \quad MA = \left ( \frac {\text {Load}}{\text {Effort}} \right )
Machines are used to get maximum mechanical advantage from them. Hence, mechanical advantage of a machine is always greater than 1 . This means that –
\quad \text {Load} \ > \ \text {Effort}
When a machine works, the effort point and load point both moves with time. The distance moved by the load point is less than distance moved by effort point. Less distance moved by load point is accompanied by the increased amount of output work or load.
Therefore, increased amount of output work which we get from a machine is in cost of proportionate decrease in the distance moved by load.
Comparison between Mechanical Advantage & Velocity Ratio
To distinguish between Mechanical advantage and Velocity ratio of a simple machine, let us consider about a straight lever as shown in figure. Here, a heavy load is being lifted from its position by use of a straight rod.
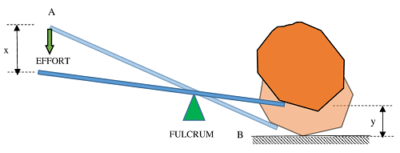
Let, ( P ) is the applied effort at the end A of the lever. Let the point A moves to a distance ( x ) downward when the load ( W ) at point B is lifted upward to a height ( y ) .
By definition, \quad \text {Work done} = \text {Force} \times \text {Displacement} .
Therefore, work input in the machine is ( P \times x ) and work output from the machine is ( W \times y )
For an ideal machine, friction is negligible. Therefore, by the law of conservation of energy we have –
\text {Input work} = \text {Output work}
Therefore, \quad P \times x = W \times y
Or, \quad \left ( \frac { W }{ P } \right ) = \left ( \frac { x }{ y } \right )
But, the term \left ( \frac { W }{ P } \right ) is the ratio of Load and Effort and called mechanical advantage of a machine.
Also, the term \left ( \frac { x }{ y } \right ) is the ratio of distance moved by effort to the distance moved by load and called velocity ratio.
Therefore, Mechanical advantage and Velocity ratio for Ideal machines are equal.
\text {Mechanical Advantage} = \text {Velocity Ratio}
But in actual conditions, all machines have friction and so a part of input work is lost in overcoming this friction.
Therefore, for actual machines, work output is always less than work input.
Or, \quad P \times x > W \times y
Therefore, \quad \left ( \frac { W }{ P } \right ) < \left ( \frac { x }{ y } \right )
Therefore, Mechanical advantage for actual machines is less than Velocity ratio.
\text {Mechanical Advantage} < \text {Velocity Ratio}
Hence, to get maximum efficiency from a machine, we have to increase the mechanical advantage to the maximum possible value.
Maximum Mechanical Advantage
Mechanical advantage of a machine is given by –
MA = \left ( \frac{ W }{ P } \right )
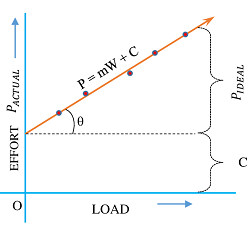
Consider about the “Load – Actual effort graph” of a machine as shown in figure.
From this graph, we get an expression for the Law of machine.
P_{Actual} = m W + C
Therefore, \quad MA = \left ( \frac { W }{ m W + C } \right ) = \left [ \frac { 1 }{ \left (m + \frac { C }{ W } \right )} \right ]
In this expression, term C represents the effect of friction and m is the slope of the graph.
If, ( W ) is too large then ratio \left ( \frac{ C }{ W } \right ) will be too small and can be neglected.
Therefore, \quad MA = \left [ \frac { 1 }{ \left (m + \frac { C }{ W } \right )} \right ] = \left ( \frac {1}{m} \right )
Thus, at much higher loads, the term \left ( \frac{ C }{ W } \right ) becomes negligible and mechanical advantage result to be maximum value of \left ( \frac { 1 }{ m } \right ) .
Therefore, maximum value of mechanical advantage is –
\quad MA_{max} = \left ( \frac { 1 }{ m } \right )
= \left ( \frac { 1 }{ \text {Slope of curve}} \right )
Maximum Efficiency
Maximum efficiency of a machine is defined as the ratio of maximum mechanical advantage and corresponding value of velocity ratio of a machine.
Therefore, \quad \eta _ {max} = \left ( \frac { MA_{max}}{ VR } \right )
= \left ( \frac { 1 }{ m } \right ) \times \left ( \frac { 1 }{ VR } \right ) = \left ( \frac { 1 }{ m \ VR } \right )
We also know that –
Efficiency \quad \eta = \left ( \frac{\text {Mechanical advantage}}{\text {Velocity ratio}} \right )
For an ideal machine, friction is zero. So –
\text {Mechanical advantage} = \text {Velocity ratio}
Therefore, efficiency of an ideal machine is ( 1 ) . Thus, we get –
\eta _ {max} = \left ( \frac { 1 }{ m \ VR } \right ) = 1
Or, \quad m \ VR = 1
So, \quad m = \left ( \frac {1}{VR} \right ) = \left ( \frac { y }{ x } \right )
Therefore, an actual machine gives maximum efficiency when the slope of the curve “load versus actual effort” is equal to the inverse of the velocity ratio of that machine.
