What is Perpendicular Axis Theorem?
Perpendicular axis theorem states that –
Moment of inertia of a laminar body about an axis which is perpendicular to the plane of the body is equal to the sum of its moments of inertia about two other axes which are on the plane of the body.
Perpendicular axis theorem is applicable for two dimensional objects to find the moment of inertia of a section about an axis perpendicular to the plane of section.
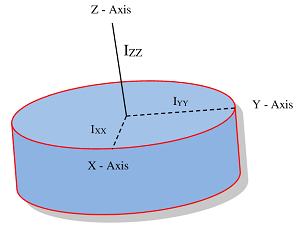
Consider about a circular disc as shown in figure. Let,
- The disc lies on XY plane.
- Moment of inertia about X axis is ( I_{xx} ) .
- Moment of inertia about Y axis is ( I_{yy} ) .
- Axis Z is another axis perpendicular to the plane of the disc and concurrent with the X and Y axes.
Therefore, according to perpendicular axis theorem –
I_{zz} = ( I_{xx} + I_{yy} )
Therefore, moment of inertia about an axis which is perpendicular to its plane is equal to the sum of its moment of inertia about two perpendicular axes on the plane of body.
Polar Moment of Inertia
Mass moment of inertia of solid objects about Z axis passing through centre of gravity is known as polar moment of inertia. It is defined as –
Polar moment of inertia is the mass moment of inertia of an object about an axis which provides resistance to torsional deformation in the object.
If moments of inertia about two axes on the plane of object and passing through centre of gravity are known, then polar moment of inertia is obtained by perpendicular axis theorem. Let, a section is laying on XY plane.
- ( I_{xx} ) and ( I_{yy} ) are the moment of inertia about X axis and Y axis respectively passing through centre of gravity.
- Then, if Z axis is the third axis passing through centre of gravity, then ( I_{zz} ) will represent the polar moment of inertia.
Therefore, by perpendicular axis theorem, polar moment of inertia will be –
I_{zz} = ( I_{xx} + I_{yy} )
Moment of Inertia of a uniform rod
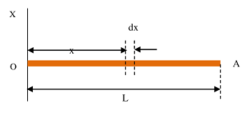
Consider about a uniform thin rod OA of length ( l ) and mass ( M ) as shown in figure.
Mass per unit length of rod will be \left ( \frac {M}{l} \right ) .
Consider an element PQ of length ( dx ) at a distance ( x ) from end O . Mass of the element will be –
dm = \left ( \frac {M}{l} \right ) dx
Moment of inertia of this element about a line OX at end O and perpendicular to the rod, will be –
dI = dm \times x^2
= \left ( \frac {M}{l} \right ) dx \ x^2
Then, by integration method, moment of inertia of whole rod about OX will be –
I_{zz} = \int dI
= \int\limits_{0}^{l} \left ( \frac {M}{l} \right ) dx \ x^2
= \left ( \frac {M}{l} \right ) \left [ \frac {l^3}{3} \right ]_{0}^{l}
= \left ( \frac {Ml^2}{3} \right )
Hence, moment of inertia of a uniform rod about an axis passing through one end of the rod is \left [ I_{zz}= \left ( \frac {Ml^2}{3} \right ) \right ]
Moment of Inertia of thin circular ring
Consider about a thin circular ring of radius ( R ) and mass ( M ) as shown in figure. Total length of ring is ( 2 \pi R ) . Therefore, mass per unit length of ring will be \left ( \frac {M}{2 \pi R} \right )
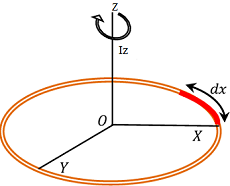
Consider about a small element PQ of length ( dx ) . Mass of this element will be –
dm = \left ( \frac {M}{2 \pi R} \right ) dx
Therefore, moment of inertia of element about ZZ axis will be –
dI = dm \times R^2
= \left ( \frac {M}{2 \pi R} \right ) dx \ R^2
= \left ( \frac {MR}{2 \pi} \right ) dx
Then, by integration method, moment of inertia of whole ring will be –
I_{zz} = \int dI
= \int\limits_{0}^{2 \pi R} \left ( \frac {MR}{2 \pi} \right ) dx
= \left ( \frac {MR}{2 \pi} \right ) \int\limits_{0}^{2 \pi R} dx
= \left ( \frac {MR}{2 \pi} \right ) \left [ x \right ]_{0}^{2 \pi R}
= \left ( \frac {MR}{2 \pi} \right ) \left [ 2 \pi R - 0 \right ]
= ( MR^2 )
Hence, moment of inertia of a uniform circular ring about an axis passing through its centre and perpendicular to the plane of the ring is \left [ I_{zz} = ( MR^2 ) \right ]
Moment of Inertia of circular disc
Consider about a uniform circular disc of radius ( R ) and mass ( M ) as shown in figure. Surface area of the disc is ( \pi R^2 ) .
Therefore, mass per unit surface area of disc will be \left ( \frac {M}{\pi R^2} \right )
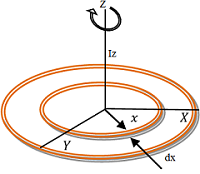
Consider about an elementary concentric ring of radius ( x ) and width ( dx ) . Surface area of the elementary ring will be ( 2 \pi x \ dx )
Then mass of the elementary ring will be –
dm = \left ( \frac {M}{ \pi R^2} \right ) 2 \pi x \ dx
= \left ( \frac {2 M x }{R^2} \right ) dx
Moment of inertia of elementary ring about ZZ' axis will be –
dI = dm \ x^2
= \left ( \frac {2 M x }{R^2} \right ) x^2 \ dx
= \left ( \frac {2 M }{R^2} \right ) x^3 \ dx
Then, by integration method, moment of inertia of whole disc will be –
I_{zz} = \int dI
= \int\limits_{0}^{R} \left ( \frac {2 M }{R^2} \right ) x^3 dx
= \left ( \frac {2M}{R^2} \right ) \int\limits_{0}^{R} x^3 dx
= \left ( \frac {2M}{R^2} \right ) \left [ \frac {x^4}{4} \right ]_{0}^{R}
= \left ( \frac {M}{2R^2} \right ) \times R^4
= \left ( \frac {MR^2}{2} \right )
Therefore, moment of inertia of a circular disc about an axis passing through the centre and perpendicular to the plane of disc is \left ( \frac {MR^2}{2} \right )
See numerical problems based on this article.
