What is dealt in study of Hydrostatics?
Hydrostatics is the branch of science which deals with the study of fluid pressure called hydrostatic pressure exerted on immersed surfaces by a liquid, when it is at rest.
- When a liquid is at rest, it exerts hydrostatic pressure on all sides of the container.
- Similarly when a surface is immersed in a liquid mass, it will experience hydrostatic pressure exerted by the liquid.
- The intensity of pressure depends upon the depth of the immersed surface from the liquid free surface.
Total Hydrostatic pressure
The total pressure on an immersed surface is defined as the total thrust exerted by the liquid on that surface. Expression for total hydrostatic pressure ( P ) is given by –
P = p_1 \ a_1 + p_2 \ a_2 + p_3 \ a_3 + ......
Where p_1, \ p_2, \ p_3, ...... are pressure head on different elemental strips of the immersed surface and a_1, \ a_2, \ a_3, ...... are areas of the corresponding strips.
Hydrostatic pressure on a vertical lamina
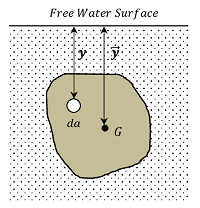
Consider about a vertical lamina of area ( A ) immersed in a liquid whose specific weight or weight per unit volume is ( w ) . Now consider an elemental area ( da ) of the lamina situated at a depth ( y ) below the free water surface as shown in figure.
The intensity of pressure acting on this elemental area will be –
p = w y
Hence, pressure force on the elemental area will be –
p = w \ y \times da
Therefore, pressure force on the whole lamina is given by –
P = \sum {w \ y \ da} = w \sum {da \ y}
But, ( \sum {da \ y} ) represents the moment of whole area of the lamina about free water surface.
So, \quad \sum {da \ y} = A \bar {y}
Where \quad \bar {y} = depth of the centroid of the lamina below the free water surface.
Hydrostatic pressure on an inclined lamina
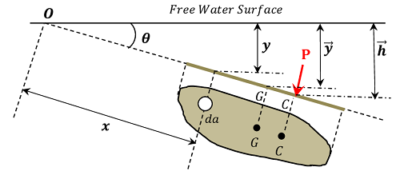
Consider about a plane inclined lamina of area ( A ) immersed in a liquid making an angle ( \theta ) with the horizontal water surface as shown in figure.
Consider an elemental area ( da ) of the lamina at a depth ( y ) below the free surface of water.
Let –
- ( w ) is specific weight of the liquid.
- ( \bar {y} ) is depth of centre of gravity G of the immersed surface from the liquid surface.
Vertical depth of the elemental area from liquid free surface is ( y = x \sin \theta )
Hence, hydrostatic pressure on the element is = w \ y \ da
Therefore, total pressure on the surface is found out by integration over the entire surface.
P = \sum {w \ y \ da} = w \sum {da \ y}
Therefore, \quad P = w A \bar y
Hydrostatic pressure on a curved surface
Hydrostatic pressure on a curved surface is obtained by calculating the horizontal and vertical component forces on the surface which are then combined together to give the total pressure.
Consider about a curved surface AB immersed in a liquid as shown in figure.
In figure (A), the liquid pressure is on the concave side of curved surface. In figure (B), the liquid pressure is on the convex side of curved surface.
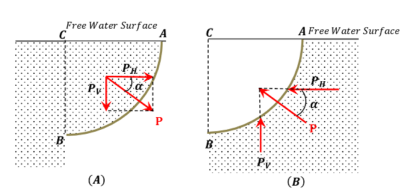
Let, BC is the vertical projection and AC is the horizontal projection of surface.
- The horizontal component ( P_H ) of pressure will be the total horizontal pressure on the projection BC of the curved surface and will act through the centre of pressure of the surface.
- The vertical component ( P_V ) of pressure will be the total weight of the liquid in the portion ABC and will act through the centre of gravity of the liquid volume ABC .
Now the total pressure or the resultant pressure may be found out by the relation –
P = \sqrt {{P_H}^2 + {P_V}^2}
The inclination of the resultant pressure with the horizontal component will be given by the relation –
\tan \alpha = \frac {P_V}{P_H}
Sometimes, the curved surface is subjected to hydrostatic pressure on its lower side (convex side) as shown in figure (B). While its upper side is not subjected to such pressure. In such cases, the vertical pressure ( P_V ) will be equal to the weight of the imaginary volume of liquid above this lower surface and up to the free surface of liquid. In such cases the direction of ( P_V ) will be upwards. The inclination of the resultant pressure may be found out as usual.
