What is called Electrostatic Force?
Static charge of a body is the fundamental physical property of a matter that causes to feel a force of attraction or repulsion due to another charged body. This force of attraction or repulsion between charged bodies is called electrostatic force.
Magnitude of electrostatic force was first formulated by Coulomb. Hence, it is also called Coulomb’s force. The force of attraction between two static charges is measured by using a device called Torsion balance.
Coulomb’s law of Electrostatic Force
Coulomb establishes an expression for electrostatic force of attraction or repulsion between static charges. Coulombs law states that –
The magnitude of force of attraction or repulsion between two point charges is –
- Directly proportional to the product of the magnitude of charges.
- Inversely proportional to the square of the distance between the charges.
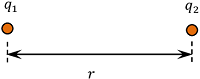
Consider about two point charges ( q_1 ) and ( q_2 ) which are kept at a distance of ( r ) as shown in figure.
Then, by Coulomb’s law –
- F \propto q_1 q_2
- F \propto \left ( \frac {1}{r^2} \right )
Therefore, force between two charges will be –
F \propto \left ( \frac { q_1 q_2 } { r^2 } \right )
Or, \quad F = k \left ( \frac { q_1 q_2 } { r^2 } \right )
The force ( F ) is called electrostatic force or Coulomb’s force and ( k ) is a constant of proportionality called Coulomb’s constant.
The value of Coulomb’s constant ( k ) depends upon –
- The system of units used for charges and
- The nature i.e. permittivity of medium in which the charges are kept.
In SI system of units –
k = \left ( \frac {1}{4 \pi \epsilon} \right ) = \left ( \frac {1}{4 \pi \epsilon_0 \epsilon_r} \right )
Where, ( \epsilon ) is the permittivity of the medium, ( \epsilon_0 ) is the absolute permittivity of free space and ( \epsilon_r ) is the relative permittivity of the medium with respect to free space.
Therefore, \quad \epsilon = \left ( \epsilon_0 \times \epsilon_r \right )
The value of absolute permittivity of free space is –
\epsilon_0 = 8.854 \times 10^{-12} \ C^2 \ N^{-1} \ m^{-2}
Characteristics of Electrostatic Force
Electrostatic force has the following characteristics –
- It is a central force i.e. it acts along the line joining the centres of the charged particles.
- Electrostatic force is spherically symmetric because it is a function of ( r ) (distance between charges)
- Force is attractive between two unlike charges ( i.e one positive charge and other negative charge) and repulsive between two like charges ( i.e. both positive charges or both negative charges).
- Electrostatic force between two charges is not affected by the presence of other charges.
- These are conservative forces. Therefore, work done in moving a charge over a closed path in an electric field is zero.
Charge Distribution
Electrostatic force between bodies depend upon the distribution of charge on their bodies. Three types of distribution of charge is found in solid objects. These are –
- Linear charge distribution.
- Surface charge distribution.
- Volume charge distribution.
Linear Charge Distribution
One-dimensional distribution of charge is known as linear charge distribution.
This type of charge distribution is found in –
- Long wires.
- Cylindrical rods.
- Charged ring etc.
Electrostatic Force in Linear Charge Distribution
Consider about a straight wire AB of length ( l ) uniformly distributed with a total charge ( q ) as shown in figure.
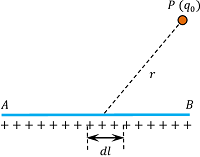
Then linear charge density on the wire will be –
\lambda = \left ( \frac {q}{l} \right )
Consider a small element of length dl of the wire. Total charge on this element will be –
dq = \lambda dl ……… (1)
Electrostatic force on a test charge q_0 placed at a point P at a distance ( r ) from the element is given by –
dF = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq \times q_0}{r^2} \right ) ……… (2)
Total force on ( q_0 ) due to charge on the whole wire will be obtained by integrating equation (2) for whole length.
Therefore, \quad F = \int\limits_{l} dF = \int\limits_{l} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq \times q_0}{r^2} \right )
Using equation (1) we have –
F = \int\limits_{l} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {\lambda dl \times q_0}{r^2} \right )
Therefore, \quad F = \left ( \frac {\lambda q_0}{4 \pi \epsilon_0} \right ) \int\limits_{l} \left ( \frac { 1 }{r^2} \right ) dl ………. (3)
Surface Charge Distribution
A two dimensional charge distributions is called surface charge distribution.
Surface charge distribution is found in –
- Thin films.
- Plane sheets etc.
Electrostatic Force in Surface Charge Distribution
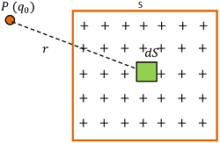
Consider a plane sheet of surface area ( S ) on which charge ( q ) is uniformly distributed as shown in figure.
Then, Surface charge density on the sheet will be –
\sigma = \left ( \frac {q}{S} \right )
Consider a small element of area ( dS ) of the sheet. Total charge on this element will be –
dq = \sigma dS …….. (4)
Electrostatic force on a test charge ( q_0 ) placed at a point P at a distance ( r ) from the element is given by –
dF = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq \times q_0}{r^2} \right ) ………. (5)
Therefore, total force on charge ( q_0 ) due to charge on the whole sheet is obtained by integrating equation (5) for whole surface.
Therefore, \quad F = \int\limits_{S} dF = \int\limits_{S} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq \times q_0}{r^2} \right )
Using equation (4) we have –
F = \int\limits_{S} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {\sigma dS \times q_0}{r^2} \right )
Therefore, \quad F = \left ( \frac {\sigma q_0}{4 \pi \epsilon_0} \right ) \int\limits_{S} \left ( \frac { 1 }{r^2} \right ) dS ………. (6)
Volume Charge Distribution
Volume charge distribution is a three dimensional charge distributions.
This type of charge distribution is found in –
- Solid objects.
- Charge on a bulb.
- Sphere etc.
Electrostatic Force in Volume Charge Distribution –
Consider about a solid object of volume ( V ) on which charge ( q ) is uniformly distributed as shown in figure.
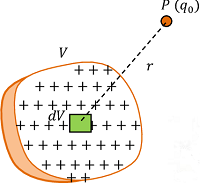
Then, volume charge density on the object will be –
\rho = \left ( \frac {q}{V} \right )
Consider a small element of volume ( dV ) of the object. Total charge on this element will be –
dq = \rho dV ……… (7)
Electrostatic force on a test charge ( q_0 ) placed at a point P at a distance ( r ) from the element is given by –
dF = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq \times q_0}{r^2} \right ) ………. (8)
Therefore, total force on ( q_0 ) due to charge on the whole object is obtained by integrating the equation (8) for whole object.
F = \int\limits_{V} dF = \int\limits_{V} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq \times q_0}{r^2} \right )
Using equation (7) we will get –
F = \int\limits_{V} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {\rho dV \times q_0}{r^2} \right )
Therefore, \quad F = \left ( \frac {\rho q_0}{4 \pi \epsilon_0} \right ) \int\limits_{V} \left ( \frac { 1 }{r^2} \right ) dV ………. (9)
See numerical problems based on this article.
