Gauss Law & Flux

What is called Gauss Law?

Gauss law gives a relation between a charged body and its associated electric flux. This law states that –

The total electric flux through any imaginary closed surface ( called Gaussian surface ) in free space is equal to the $( \frac {1}{\epsilon_0} )$ times of the total electric charge enclosed by that surface.

Therefore, $\quad \phi = \oint\limits_{S} \vec {E}. d \vec {S} = \left ( \frac {1}{\epsilon_0} \right ) q$

$= \left ( \frac {q}{\epsilon_0} \right )$

Here, $( \vec {E} )$ represents the electric field vector and $( \vec {S} )$ represents the surface area vector.

Gauss law is applicable for any type of charge distribution i.e. a point charge or an uniformly distributed charge. The chosen Gaussian surface must be uniformly spaced around the charge under consideration. Gaussian surface should be so chosen such that all points on its surface are equidistant from the enclosed charge. Hence a Gaussian surface is taken as a regular geometrical shapes viz. a sphere, a cylinder, a cuboid, an octahedron etc.

Sign of Electric Flux

From earlier discussions of electric field lines developed by point charges and electric flux, we know that –

A positive charge develops diverging field lines. Hence, outward electric flux through a closed Gussian surface is taken as positive.

Therefore, $\quad \phi = \oint\limits_{S} \vec {E}. \vec {dS} = \left ( \frac {+ q}{\epsilon_0} \right )$

A negative charge develops converging field lines. Hence, inward electric flux through a closed surface is taken as negative.

Therefore, $\quad \phi = \oint\limits_{S} \vec {E}. \vec {dS} = \left ( \frac {- q}{\epsilon_0} \right )$

Gaussian Surface

Gaussian surface around a charge is an imaginary closed surface such that the intensity of electric field at all points on this surface is same.

Intensity of electric field at a point around a charged particle is given by –

$E \propto \left ( \frac {1}{r^2} \right )$ .

Illustration of Gauss Law

Consider about following illustrative conditions explaining the application of gauss law. In given illustrative figures, the dotted circles represent Gaussian surfaces.

Condition – 1

If the closed Gaussian surface does not include any charge then net flux through this surface is zero.

070701 NO EFFECT OF CHARGE KEPT OUTSIDE OF GAUSSIAN SURFACE

Therefore, when $( q = 0 )$ then $( \phi = 0 )$

Condition – 2

A charge which is placed outside the closed Gaussian surface will not effect the net electric flux from the surface.

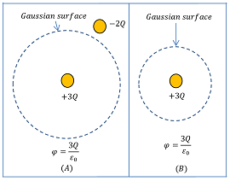
Consider about a set up as shown in figure (A). In adjoining figure, the net charge inside closed gaussian surface is $( + 3 Q )$ . Another charge $( - 2 Q )$ is also present nearby but it is outside of the Gaussian surface.

Therefore, as per Gauss law, the charge $( - 2 Q )$ will have no effect on the total flux through the surface. So, in this case total flux will be –

$\phi = \left ( \frac { 3 Q }{\epsilon_0} \right )$ .

This amount of flux is coming out through the whole Gaussian surface from all around.

Condition – 3

Net electric flux through a closed Gaussian surface is directly proportional to the net amount of charge enclosed within the surface but it is independent of the size of the closed surface.

Consider about the set up as shown in figure (B). It is similar to the set up in figure (A) only the difference is in the size of Gaussian surface which is now taken of a smaller size. Here, also the net charge inside the closed surface is $( + 3 Q )$ .

Therefore, $\phi = \left ( \frac { 3 Q }{\epsilon_0} \right )$ .

This amount of flux is coming out through the whole Gaussian surface from all around.

Condition – 4

If the closed surface contains two charges of equal magnitude but opposite in sign then the net flux through the surface is zero.

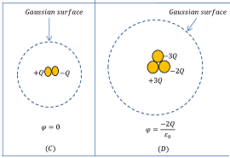
070702 EFFECT OF TOTAL CHARGE INSIDE GAUSSIAN SURFACE

Consider about a set up as shown in figure (C). Two unlike charges of equal magnitude are placed inside the Gaussian surface.

Net charge inside the closed surface is $( + Q - Q ) = 0$ .

Therefore, $\quad \phi = 0$

Condition – 5

If the closed Gaussian surface contains many charges of different magnitudes then flux will be in accordance with the additive property of electrical charges inside the closed surface.

Consider about the set up as shown in figure (D). Let, three charges $(+ 3Q ), \ ( - 2Q ) \ \text {and} \ ( - 3Q )$ are placed inside the closed Gaussian surface. Net or total charge inside the closed surface is $\left ( + 3Q - 2Q - 3 Q \right ) = ( - 2Q )$ .

Therefore, $\quad \phi = \left ( \frac {- 2Q}{\epsilon_0} \right )$ .

This is inward flow of flux i.e. this amount of total flux is penetrating and going inside the Gaussian surface from outside space.

Application of Gauss Law

Gauss law helps in evaluating the electric field of bodies having continuous charge distribution like a charged wire, charged thin sheet, charged sphere etc.

Gauss law is very helpful and applied to find the electric field of charged bodies in a very convenient way in following cases –