How to find Centre of Mass of Solid Hemisphere?
A solid hemispherical body may be considered to be constructed of numerous tiny particles. These tiny particles have their own masses. Hence, the total mass of the hemisphere is equal to the sum of all tiny masses by which the cone is made up of.
By gravitational nature of earth, each of these tiny particles is attracted towards the centre of the earth with a gravitational force, which is proportional to its mass. This is called weight of particles.
Weight of each tiny particle acts towards the centre of the earth. Therefore, these tiny weights form a system of parallel forces whose direction is towards the centre of earth. The centre of these parallel forces is called the centre of mass of the hemispherical body.
Centre of mass of a hemispherical solid is determined by integration method as follows –
STEP – 1
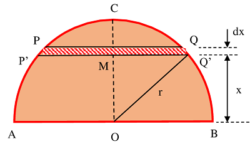
Consider about a solid hemisphere ACB as shown in figure. Let, radius of hemisphere is ( OB = r ) .
Hemisphere is symmetrical about its vertical axis ( OC ) . Hence, ( \bar {x} ) co-ordinate of centre of mass will lie on line ( OC ) .
STEP – 2
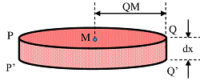
Two cutting planes PQ and P'Q' , separated by a distance ( dx ) and parallel to the base AB are used to cut an element circular disc PP'Q'Q from the hemisphere. Let, the plane P'Q' is at a distance ( x ) from the base AB .
Therefore, thickness of the cut out circular element PP'Q'Q will be ( dx ) . Let, the centre of the cut out element is at M and its distance from base is ( x ) .
STEP – 3
From geometry of the hemisphere, we will get –
QM^2 = ( OQ^2 - OM^2 ) = ( r^2 - x^2 )
Let, ( \rho ) is the density of material of hemisphere. Then, mass of elementary disc will be –
\text {Mass of element} = \text {Volume} \times \text {Density} = \text {Area} \times \text {Thickness} \times \text {Density}
So, \quad dm = \pi \ ( QM^2 ) \ \times dx \ \times \ \rho
= \pi \ ( r^2 - x^2 ) \ dx \ \rho
Then, moment of elementary mass of disc about point O will be –
dM = dm . x
= \pi \ ( r^2 - x^2 ) \ dx \ \rho \ x
The centre of mass of element will lie at its geometrical centroid at M .
STEP – 4 & 5
Then by definition, the centre of gravity of solid hemisphere from base AB will be –
\bar {y} = \frac {\text {Moment of all elementary masses about point O}}{\text {Total mass}}
= \left [ \frac { \sum_{0}^{r} \pi \ ( r^2 - x^2 ) dx \ \rho \ x }{ \sum_{0}^{r} \pi \ ( r^2 - x^2 ) dx \ \rho } \right ]
= \left [ \frac { \int\limits_{0}^{r} \pi \ ( r^2 - x^2 ) dx \ x }{ \int\limits_{0}^{r} \pi \ ( r^2 - x^2 ) dx } \right ]
= \left [ \left ( \frac { r^2 x^2 }{ 2 } \right ) - \left ( \frac { x^4 }{ 4 } \right ) \right ]_{ 0 }^{ r } \div \left [ ( r^2 x ) - \left ( \frac { x^3 }{ 3 } \right ) \right ]_{ 0 }^{ r }
= \left ( \frac { r^4 }{ 4 } \right ) \div \left ( \frac { 2r^3 }{ 3 } \right )
= \left ( \frac { 3r }{ 8 } \right )
Therefore, centre of mass of a solid hemisphere lies on its central radius OC at a distance \left ( \frac {3r}{8} \right ) from plane of base.
Centre of Mass of a Hollow Hemisphere
Centre of mass of hollow circular cone is also determined by integration method as follows –
STEP – 1
Consider about a hollow thin hemispherical shell ACB as shown in figure. Let radius of hemisphere is ( R ) .
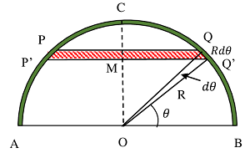
Hollow hemispherical shell is symmetrical about vertical axis ( OC ) . Hence, ( \bar {x} ) co-ordinate of centre of mass will lie on axis ( OC ) .
STEP – 2
Consider about an elementary circular ring PP'Q'Q cut off by two planes at angular distances ( \theta ) from base radius OB .
Width of the circular elemental ring subtend an angle of ( d \theta ) at origin O . Width of ring will be ( dx = R d \theta )
STEP – 3
From geometry of the hemispherical shell, radius of elementary ring QM = ( R \cos \theta )
Let, ( \sigma ) is the mass per unit area of material of hemisphere.
Then mass of elementary ring will be –
\text {Mass of element} = \text {Area of element} \times \text {Mass per unit area} = \text {Circumference} \times \text {Width} \times \text {Mass per unit area}
So, \quad dm = 2 \pi \ ( QM ) \ \times \ dx \ \times \ \sigma
= 2 \pi \ \sigma \ ( R \cos \theta ) \ ( R d \theta ) = 2 \pi \ \sigma \ R^2 \ \cos \theta \ d \theta
Also, total surface area of hemispherical shell is ( 2 \pi R^2 ) . Let, total mass of the hemispherical shell is ( M_{shell} ) . Then –
\sigma = \left ( \frac {M_{shell}}{2 \pi R^2} \right )
Putting this value, we get –
dm = 2 \pi \ \left ( \frac {M_{shell}}{2 \pi R^2} \right ) \ R^2 \ \cos \theta \ d \theta
= ( M_{shell} \cos \theta \ d \theta )
Centre of mass of the elementary ring is at M and it is at distance ( OM = R \sin \theta ) from point O .
Moment of the elementary ring about O will be –
d M = dm \times ( OM ) = ( M_{shell} \cos \theta \ d \theta ) \times ( R \sin \theta )
= R ( M_{shell} \cos \theta \ \sin \theta d \theta )
= \left ( \frac {R}{2} M_{shell} \right ) \left ( 2 \sin \theta \ \cos \theta d \theta \right )
= \left ( \frac {R}{2} M_{shell} \right ) \left ( \sin 2 \theta \ d \theta \right )
STEP – 4 & 5
Then by definition, the centre of gravity of hemispherical shell from O will be –
\bar {y} = \frac {\text {Moment of all elementary masses about point O}}{\text {Total mass}}
= \left [ \frac { \sum_{0}^{\pi / 2} dM}{ M_{shell} } \right ]
= \left [ \frac { \sum_{0}^{\pi / 2} \left ( \frac {R}{2} M_{shell} \right ) \sin 2 \theta \ d \theta )}{ M_{shell} } \right ]
= \left [ \left ( \frac {R}{2} \right ) \int\limits_{0}^{\pi / 2} \sin 2 \theta \ d \theta \right ]
= \left ( \frac {R}{2} \right ) \left [ - \cos 2 \theta \right ]_{0}^{\pi / 2}
= - \left ( \frac {R}{2} \right ) ( 0 - 1 )
= \left ( \frac {R}{2} \right )
Therefore, centre of gravity of a hollow hemisphere lies on the central radius at a distance \left ( \frac {R}{2} \right ) from the plane of base.
Centre of Mass of Semi-circular Arc
Consider about a semi circular arc ACB of radius ( r ) as shown in figure. Semi-circular arc is symmetrical about vertical line ( OC ) . Hence, ( \bar {x} ) co-ordinate will lie on line ( OC ) .
Consider about an elementary arc P at an angular distance ( \theta ) from central radius OC and subtending an angle ( d \theta ) at O .
Length of the elementary arc P is ( r d \theta ) . Also distance of arc P from AB is ( r \sin \theta ) .
Let, ( \sigma ) is the mass per unit length of the arc material. Then, mass of the elementary arc will be –
\text {Mass} = \text {Length of arc} \times \text {Mass per unit length}
Or, \quad dm = ( r d \theta \sigma ) = ( r \sigma d \theta )
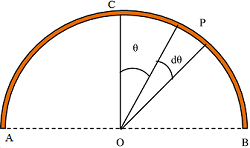
Moment of elementary arc P about O will be –
dM = ( r d \theta \sigma ) \times ( r \sin \theta ) = ( r^2 \sigma d \theta \sin \theta )
By definition, distance of centre of mass of semi circular arc from O will be –
\bar {y} = \frac {\text {Moment of all elementary masses about point O}}{\text {Total mass}}
=\left [ \frac { \int\limits_{- \frac {\pi}{2}}^{\frac {\pi}{2}} ( r^2 \sigma d \theta \sin \theta ) }{ \int\limits_{- \frac {\pi}{2}}^{\frac {\pi}{2}} ( r \sigma d \theta ) } \right ]
= \left [ r \left ( - \cos \theta \right )_{- \frac {\pi}{2}}^{\frac {\pi}{2}} \right ] \div \left [ \left ( \theta \right )_{ - \frac {\pi}{2}}^{\frac {\pi}{2}} \right ]
= \left ( \frac {2r}{\pi} \right )
Therefore, centre of mass of a semi circular arc lies at a distance of \left ( \frac {2r}{\pi} \right ) from point O .
Motion of Centre of Mass
Consider about a system of ( n ) numbers of masses of quantity ( m_1, \ m_2, \ ....... m_n ) etc. Suppose that, forces ( F_1, \ F_2, \ ....... F_n ) etc. are acting on them to produce accelerations ( a_1, \ a_2, \ ....... a_n ) etc. respectively.
Since, no other external force is acting on the system, therefore –
F_{Total} = 0
So, \quad ( F_1 + F_2 + ....... + F_n ) = 0
Therefore, \quad ( m_1 a_1 + m_2 a_2 + ....... + m_n a_n ) = 0
Or, \quad \left [ m_1 \left ( \frac {dv_1}{dt} \right ) + m_2 \left ( \frac {dv_2}{dt} \right ) + ....... + m_n \left ( \frac {dv_n}{dt} \right ) \right ] = 0
Or, \quad \left ( \frac {d}{dt} \right ) \left [ ( m_1 v_1 ) + ( m_2 v_2 ) + ....... + ( m_n v_n ) \right ] = 0
We know that, differential of a constant term is zero.
Therefore, \quad \left [ ( m_1 v_1 ) + ( m_2 v_2 ) + ....... + ( m_n v_n ) \right ] = Constant.
But, ( m v = p ) is the linear momentum of individual particles.
So, \quad ( p_1 + p_2 + ....... + p_n ) = Constant.
Or, \quad p_{Total} = Constant.
Hence, in absence of any external force, the total linear momentum of a moving system of masses is conserved. This is known as the law of conservation of momentum.
Also, \quad p_{Total} = M v_{com}
Here, ( v_{com} ) is the velocity of centre of mass and ( M ) is the total mass of the system.
Therefore, \quad v_{com} = Constant.
Hence, in absence of any external force, the velocity of centre of mass of a body remains constant.
See numerical problems based on this article.
