What are called Capacitor & Capacitance?
A capacitor is defined as a combination of two conducting surfaces separated by a non conducting medium such that it can store electric charge.
When two conducting surfaces of a capacitor are connected to the two terminals of a battery, the surfaces get charged by charges of equal magnitude but opposite in sign. This is called charging of a capacitor.
When the battery is disconnected after charging, the charges on the conducting surfaces remains the same. Hence, a capacitor stores the charge.
The potential difference between the conducting surfaces of a capacitor is the potential difference of the connected battery. The charges developed on the conducting surfaces will be –
q \propto V
Or, \quad q = C V …….. (1)
Capacitance of Capacitor
Charge developed on the plates is proportional to the applied potential difference between them.
Therefore, \quad q = C V . Here, ( C ) is a constant of proportionality and called Capacitance.
Therefore, \quad C = \left ( \frac {q}{V} \right ) ………. (2)
Thus, capacitance ( C ) is defined by the ratio of the magnitude of the charge ( q ) ( on one of the surface ) to the potential difference ( V ) between the surfaces.
Energy stored in a Capacitor
Consider about charging of a capacitor as shown in figure. Charging is similar to the transfer of charges from one plate to another plate of a capacitor. Therefore, some work is done in transferring these charges. This work done is stored as a potential energy in the capacitor.
Let, at any instant, the charge on one of the plate is ( q ) .
- Then capacitance will be –
C = \left ( \frac {q}{V} \right )
Or, \quad V = \left ( \frac {q}{C} \right )
If extra charge ( dq ) is transferred to the plates, then work done –
dW = V dq = \left ( \frac {q}{C} \right ) dq ………. (1)
Total increase in potential energy in charging of a capacitor from ( q = 0 ) to ( q = Q ) will be the total energy stored in that capacitor.
Therefore, \quad U = \int dW = \int\limits_{0}^{Q} \left ( \frac {q}{C} \right ) dq
= \left ( \frac {1}{C} \right ) \int\limits_{0}^{Q} q dq
= \left ( \frac {1}{C} \right ) \left [ \frac {q^2}{2} \right ]_{0}^{Q}
= \left ( \frac {1}{C} \right ) \left [ \frac {Q^2}{2} \right ] = \left ( \frac {Q^2}{2C} \right )
= \left ( \frac {1}{2} \right ) \left ( \frac {Q^2}{C} \right ) ………. (2)
This gives the expression for energy stored in a capacitor.
Effect of Dielectric on energy of a Capacitor
Inserting of a dielectric slab between the plates of parallel plate capacitor, increases its capacitance.
If a parallel plate capacitor has capacitance ( C_0 ) and if a dielectric substance of dielectric constant ( K ) is inserted between the plates, then final capacitance will be –
C = K C_0
Therefore, introduction of dielectric substance increases the energy storing capacity.
Now, consider about two instances producing different results (1) dielectric slab is inserted disconnecting the battery (2) dielectric slab is inserted with battery connected.
Dielectric inserted, when battery is disconnected
Consider a capacitor of capacitance ( C_0 ) and charge ( Q_0 ) in the absence of any dielectric medium between the plates. Then, energy stored in the capacitor will be –
U_0 = \left ( \frac {1}{2} \right ) \left ( \frac {Q^2_0}{C_0} \right ) ……. (1)
= \left ( \frac {1}{2} \right ) \left ( \frac {C^2_0 V^2}{C_0} \right )
= \left ( \frac {1}{2} \right ) C_0 V^2 ………. (2)
When battery is disconnected and a dielectric substance of dielectric constant ( K ) is inserted between the plates, then –
- Feeding of extra charge is disconnected from the source of supply. Hence, charge on the plates remains the same. So, ( Q = Q_0 ) .
- But, capacitance of the capacitor increases due to insertion of dielectric. So, ( C = K C_0 )
Therefore, energy stored will be –
U = \left ( \frac {1}{2} \right ) \left ( \frac {Q^2}{C} \right ) = \left ( \frac {1}{2} \right ) \left ( \frac {Q^2_0}{KC_0} \right )
= \left ( \frac {1}{K} \right ) \left [ \left ( \frac {1}{2} \right ) \left ( \frac {Q^2_0}{C_0} \right ) \right ]
= \left ( \frac {1}{K} \right ) U_0 ……….. (3)
Therefore, \quad U = \left ( \frac {U_0}{K} \right )
Since, ( K > 1 ) . Therefore, ( U < U_0 )
Thus, energy stored in the capacitor has got decreases.
Thus, energy stored in a capacitor decreases when a dielectric slab is inserted between the plates of capacitor while disconnecting the battery.
Dielectric inserted, when battery is in connection
Now, consider about a capacitor of capacitance ( C_0 ) and charge ( Q_0 ) in the absence of any dielectric medium between the plates. When battery is connected and a dielectric slab of dielectric constant ( K ) is inserted between the plates –
- Battery transfers extra charge. So, charge on the capacitor becomes ( Q = K Q_0 ) .
- The capacitance also becomes ( C = K C_0 )
Therefore, energy stored in the capacitor –
U = \left ( \frac {1}{2} \right ) \left ( \frac {Q^2}{C} \right ) = \left ( \frac {1}{2} \right ) \left ( \frac {K^2 Q^2_0}{KC_0} \right )
= K \left [ \left ( \frac {1}{2} \right ) \left ( \frac {Q^2_0}{C_0} \right ) \right ]
Therefore, \quad U = K U_0 ………. (2)
Also, \quad U = \left ( \frac {1}{2} CV^2 \right ) = \left ( \frac {1}{2} \right ) \left ( \frac {K^2 Q^2_0}{KC_0} \right )
= \left ( \frac {1}{2} \right ) \left ( \frac {K^2 C^2_0 V^2}{K C_0} \right ) = \left ( \frac {1}{2} \right ) K C_0 V^2 …….. (3)
Since, ( K > 1 ) . Therefore ( U > U_0 )
Thus, energy stored in capacitor has got increases.
Thus energy stored in a capacitor increases when a dielectric slab is inserted between the plates of capacitor without disconnecting the battery.
Combination of Capacitors
When a combination of two or more capacitors are used in an electrical circuit, we can replace the combination of capacitors with a single capacitor called equivalent capacitor.
The capacitance of equivalent capacitor is called equivalent capacitance.
Capacitors can be grouped in three ways –
- Series combination.
- Parallel combination.
- Mixed combination.
Capacitors in Series
Consider about three capacitors of capacitance C_1, \ C_2 \ \text {and} \ C_3 which are connected in series between points A and B as shown in figure.
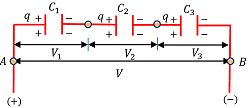
Total potential difference V across this arrangement will be divided as V_1, \ V_2 \ \text {and} \ V_3 across each capacitor but the charge on each capacitor remains the same.
Therefore, \quad V = ( V_1 + V_2 + V_3 ) …… (1)
But, \quad V_1 = \left ( \frac {q}{C_1} \right ) \quad V_2 = \left ( \frac {q}{C_2} \right ) \quad \text {and} \quad V_3 = \left ( \frac {q}{C_3} \right ) .
Where, ( q ) is the charge on each capacitor. Therefore, equation (1) becomes –
V = \left [ \left ( \frac {q}{C_1} \right ) + \left ( \frac {q}{C_2} \right ) + \left ( \frac {q}{C_3} \right ) \right ]
= q \left [ \left ( \frac {1}{C_1} \right ) + \left ( \frac {1}{C_2} \right ) + \left ( \frac {1}{C_3} \right ) \right ] ……….. (2)
Let, ( C ) is the equivalent capacitance of the series combination of the capacitors –
Then, \quad C = \left ( \frac {q}{C} \right )
So, \quad \left ( \frac {q}{C} \right ) = q \left [ \left ( \frac {1}{C_1} \right ) + \left ( \frac {1}{C_2} \right ) + \left ( \frac {1}{C_3} \right ) \right ]
Or, \quad \left ( \frac {1}{C} \right ) = \left [ \left ( \frac {1}{C_1} \right ) + \left ( \frac {1}{C_2} \right ) + \left ( \frac {1}{C_3} \right ) \right ]
Therefore, in series combination of capacitors, the reciprocal of equivalent capacitance is equal to the sum of the reciprocals of capacitance of individual capacitors.
Capacitors in Parallel
Consider about three capacitors of capacitance C_1, \ C_2 \ \text {and} \ C_3 which are connected in parallel between two points A and B as shown in figure.
Total potential difference V across the points A and B remains same for all capacitors but total charge ( q ) is divided in q_1, \ q_2 \ \text {and} \ q_3 across each capacitor respectively.
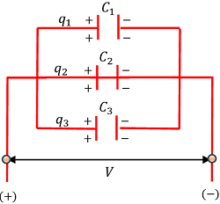
Therefore, \quad q = ( q_1 + q_2 + q_3 )
But, \quad q_1 = ( C_1 V ) \quad q_2 = ( C_2 V ) \quad \& \ q_3 = ( C_3 V ) . Therefore, \quad q = V \left ( C_1 + C_2 + C_3 \right ) …….. (1)
Let, ( C ) is the equivalent capacitance of the parallel combination of the capacitors. Then, \quad q = CV
Hence, equation (1) becomes –
C V = \left ( C_1 + C_2 + C_3 \right ) V
So, \quad C = \left ( C_1 + C_2 + C_3 \right ) ………. (2)
Therefore, in parallel combination of capacitors, the equivalent capacitance is equal to the sum of the capacitances of individual capacitors.
See numerical problems based on this article.
