Elastic Collision

What is called an Elastic Collision?

Collision is an event in which two moving bodies or one moving body and other stationary body collide (strike) with each other.

In an elastic collision –

Momentum is conserved.
Kinetic energy is conserved.
All forces acting on the system are conservative forces.

Properties of Elastic Collision

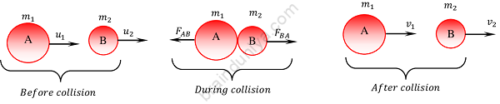
Consider about two elastic bodies $( A )$ and $( B )$ of masses $( m_1 )$ and $( m_2 )$ which are moving along the same straight line with velocities $( u_1 )$ and $( u_2 )$ respectively. Assume that $[ ( u_1 ) \ > \ ( u_2 ) ]$ .

After some time, the two bodies will collide head-on and continue moving in the same direction with final velocities $( v_1 )$ and $( v_2 )$ respectively. After collision, the two bodies will separate if $[ ( v_2 ) \ > \ ( v_1 ) ]$ .

Conservation of Momentum

By law of conservation of momentum, we get –

$( m_1 u_1 ) + ( m_2 u_2 ) = ( m_1 v_1 ) + ( m_2 v_2 )$ …….. (1)

Or, $\quad ( m_1 u_1 ) - ( m_1 v_1 ) = ( m_2 v_2 ) - ( m_2 u_2 )$

Or, $\quad [ m_1 ( u_1 - v_1 ) ] = [ m_2 ( v_2 - u_2 ) ]$ ……. (2)

040901 CONSERVATION IN ELASTIC COLLISION

Conservation of Energy

By law of conservation of kinetic energy, we get –

$\left [ \left ( \frac {1}{2} \right ) m_1 u^2_1 + \left ( \frac {1}{2} \right ) m_2 u^2_2 \right ] = \left [ \left ( \frac {1}{2} \right ) m_1 v^2_1 + \left ( \frac {1}{2} \right ) m_2 v^2_2 \right ]$

Or, $\quad \left ( m_1 u^2_1 - m_1 v^2_1 \right ) = \left ( m_2 v^2_2 - m_2 u^2_2 \right )$

Or, $\quad \left [ m_1 ( u_1 + v_1 )( u_1 - v_1 ) \right ] = \left [ m_2 ( v_2 + u_2 )( v_2 - u_2 ) \right ]$ …… (3)

Dividing equation (3) by (2), we get –

$( u_1 + v_1 ) = ( v_2 + u_2 )$

Or, $\quad ( u_1 - u_2 ) = ( v_2 - v_1 )$ …… (4)

Therefore, Relative velocity of $A$ with respect to $B$ before collision = Relative velocity of $B$ with respect to $A$ after collision.

This is also termed as –

$\text {Relative velocity of approach} = \text {Relative velocity of separation}$

Velocities after Collision

For elastic collision, we know –

$( u_1 - u_2 ) = ( v_2 - v_1 )$

Or, $\quad v_2 = ( u_1 - u_2 ) + v_1$

Putting this value of $( v_2 )$ in equation (1), we will get –

$( m_1 u_1 ) + ( m_2 u_2 ) = ( m_1 v_1 ) + [ m_2 ( u_1 - u_2 )+ v_1 ]$

Or, $\quad ( m_1 u_1 ) + ( m_2 u_2 ) = ( m_1 v_1 + m_2 u_1 - m_2 u_2 + m_2 v_1 )$

Or, $\quad ( m_1 - m_2 ) u_1 + 2 m_2 u_2 = ( m_1 + m_2 ) v_1$

Therefore, $\quad v_1 = u_1 \left [ \frac { ( m_1 - m_2 ) }{ ( m_1 + m_2 ) } \right ] + u_2 \left [ \frac { 2 m_2 }{ ( m_1 + m_2 ) } \right ]$ ……. (5)
Similarly, $\quad v_2 = u_2 \left [ \frac { ( m_2 - m_1 ) }{ ( m_1 + m_2 ) } \right ] + u_1 \left [ \frac { 2 m_1 }{ ( m_1 + m_2 ) } \right ]$ ……. (6)

Collision between equal mass bodies

CASE 1 – When both the bodies were initially moving.

For collision between equal mass bodies, $\quad m_1 = m_2 = m$ (say).

Then from equation (5), we get –

$v_1 = \left [ 0 + u_2 \left ( \frac { 2 m }{ m + m } \right ) \right ] = u_2$

And from equation (6), we get –

$v_2 = \left [ 0 + u_1 \left ( \frac { 2 m }{ m + m } \right ) \right ] = u_1$

Hence, when two bodies of equal masses collide in elastic collision, their velocities get exchanged after the collision.

CASE 2 – When one of the body was initially at rest.

Let, the body $( B )$ is in rest. Then $( u_2 = 0 )$

Then from equation (5), we get –

$v_1 = \left [ 0 + 0 \times \left ( \frac { 2 m }{ m + m } \right ) \right ] = 0$

And from equation (6), we get –

$v_2 = \left [ 0 + u_1 \left ( \frac { 2 m }{ m + m } \right ) \right ] = u_1$

Hence, when an elastic body collides against another elastic body of equal mass at rest, then after collision the first body comes to rest while the second body moves with the velocity of the first.

CASE 3 – When a very light body collides against a massive stationary body.

Consider that, $[ ( m_1 ) << ( m_2 ) ]$ , so we can neglect the mass $( m_1 )$ . Also $( u_2 = 0 )$

Then from equation (5), we get –

$v_1 = \left [ u_1 \left ( \frac { - m_2 }{ m_2 } \right ) + 0 \right ] = - u_1$

And from equation (6), we get –

$v_2 = \left [ 0 + u_1 \left ( \frac { 0 }{ m_2 } \right ) \right ] = 0$

Hence, when a light body collides with a massive body at rest, the light body rebounds after the collision with an equal and opposite velocity but the massive body remains stationary as it was before collision.

CASE 4 – When a massive body collides against a stationary light body.

Consider that, $[ ( m_1 ) >> ( m_2 ) ]$ , so we can neglect the mass $( m_2 )$ . Also $( u_2 = 0 )$

Then from equation (5), we get –

$v_1 = u_1 \left [ \left ( \frac { m_1 }{ m_1 } \right ) + 0 \right ] = u_1$

And from equation (6), we get –

$v_2 = \left [ 0 + u_1 \left ( \frac { 2 m_1 }{ m_1 } \right ) \right ] = 2 u_1$

Hence, when a massive body collides with a light body at rest, then the velocity of massive body remains unchanged while the light body starts moving with twice the velocity of massive body after the collision.

In-elastic Collision

In an in-elastic collision –

Momentum is conserved.
Loss in kinetic energy takes place in the form of heat, light or sound.
Some or all of the involved forces are non conservative forces.

Properties of in-elastic Collision

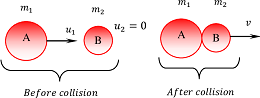
Consider that a body of mass $( m_1 )$ moving with velocity $( u_1 )$ collides head-on with another body of mass $( m_2 )$ at rest. After the collision, the two bodies will move together with a common velocity $( v )$ .

040902 CONSERVATION IN IN-ELASTIC COLLISION

By law of conservation of momentum, we get –

$m_1 u_1 + m_2 \times 0 = ( m_1 + m_2 ) v$

Or, $\quad v = u_1 \left ( \frac {m_1}{m_1 + m_2} \right )$

Loss in kinetic energy in collision is given by –

\Delta K = ( K_i - K_f )

$= \left ( \frac {1}{2} \right ) m_1 u^2_1 - \left ( \frac {1}{2} \right ) ( m_1 + m_2 ) v^2$

$= \left ( \frac {1}{2} \right ) m_1 u^2_1 - \left ( \frac {1}{2} \right ) ( m_1 + m_2 ) \left [ \frac {m_1}{m_1 + m_2} u_1 \right ]^2$

$= \left ( \frac {1}{2} \right ) m_1 u^2_1 - \left ( \frac {1}{2} \right ) \left [ \frac {m^2_1}{( m_1 + m_2 )} \right ] u^2_1$

$= \left ( \frac {1}{2} \right ) m_1 u^2_1 \left [ 1 - \frac {m_1}{( m_1 + m_2 )} \right ]$

Or, $\quad \Delta K = \left ( \frac {1}{2} \right ) \left [ \frac {m_1 m_2}{( m_1 + m_2 ) } \right ] u^2_1$ .

Oblique Collision

In an oblique collisions –

Momentum is conserved.
Kinetic energy is conserved.

Properties of Oblique Collision

Consider that a particle of mass $( m_1 )$ moving along $X$ axis with velocity $( u_1 )$ collides with another particle of mass $( m_2 )$ at rest as shown in figure.

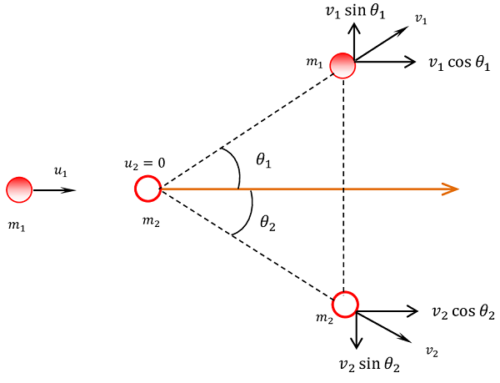
040903 CONSERVATION IN OBLIQUE COLLISION

After the collision, let the two particles move with velocities, $( v_1 )$ and $( v_2 )$ making angles $( \theta_1 )$ and $( \theta_2 )$ with $X$ axis.

By resolving the momentum after collision into rectangular components, we get –

Components of momentum of mass $( m_1 )$ are –

$( m_1 v_1 \cos \theta_1 )$ along positive $X$ axis.
$( m_1 v_1 \sin \theta_1 )$ along positive $Y$ axis.

Components of momentum of mass $( m_2 )$ are –

$( m_2 v_2 \cos \theta_2 )$ along positive $X$ axis.
$( m_2 v_2 \sin \theta_2 )$ along negative $Y$ axis.

In $X$ axis, by law of conservation of momentum, we get –

$m_1 u_1 = ( m_1 v_1 \cos \theta_1 ) + ( m_2 v_2 \cos \theta_2 )$ ……… (1)

In $Y$ axis, by law of conservation of momentum, we get –

$0 = ( m_1 v_1 \sin \theta_1 ) - ( m_2 v_2 \sin \theta_2 )$ ……… (2)

By law of conservation of kinetic energy, we get –

$\left ( \frac {1}{2} \right ) m_1 u^2_1 = \left ( \frac {1}{2} \right ) m_1 v^2_1 + \left ( \frac {1}{2} \right ) m_2 v^2_2$ ………. (3)

Coefficient of Restitution

Coefficient of restitution is defined as the ratio of the magnitude of relative velocity of separation after collision to the magnitude of relative velocity of approach before collision.

Therefore, coefficient of restitution is given by –

$e = \left [ \frac {( v_1 - v_2 )}{( u_1 - u_2 )} \right ]$

Coefficient of restitution is also called coefficient of resilience.

The value of coefficient of restitution depends upon the material of colliding bodies.

For a perfectly elastic collision $( e = 1 )$ i.e. relative velocity of separation is equal to the relative velocity of approach.
For an in-elastic collision $( 0 < e < 1 )$ i.e. relative velocity of separation is less than the relative velocity of approach.
For a perfectly in-elastic collision $( e = 0 )$ i.e. relative velocity of separation is zero. After collision the two bodies move with a common velocity.
For a super-elastic collision $( e > 1 )$ i.e. kinetic energy increases.

See numerical problems based on this article.