Metacentric Height

What is Metacentre & Metacentric height?

Metacentre is the point at which the line of action of the upthrust will meet the normal axis of a floating body, when the body is tilted by a small angle from its equilibrium position. The distance between the metacentre point $( M )$ and centre of gravity $( G )$ , is called metacentric height.

Knowing of the metacentric height of any floating body is very important, because –

Metacentric height ascertain the stability of a floating body like ships, buoys etc.
It is essential during designing of floating vessels.

Metacentre

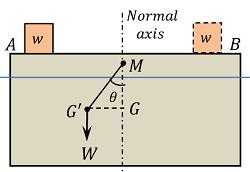
Consider about a body floating in a liquid as shown in figure.

Let, $( G )$ is the centre of gravity of the body and $( B )$ is the centre of buoyancy.

For equilibrium of the body, $( B )$ and $( G )$ must lie on same vertical line called normal axis.

Suppose, the body is given a tilt by a small angle as shown in figure (B). This tilting will produce following effects –

Because, the shape of displaced fluid changes, the centre of buoyancy will also shift to a new position at $( B_1 )$
The line of action of upthrust i.e. buoyant force is now vertical through the point $( B_1 )$
The vertical through the point $( B_1 )$ will intersect the normal axis of the body at a point $( M )$ .

This point $( M )$ is called the metacentre. It is the point which decides about the stability of any floating body. The height between the metacentre point $( M )$ and centre of gravity $( G )$ of the body is called the metacentric height.

Equilibrium of floating bodies

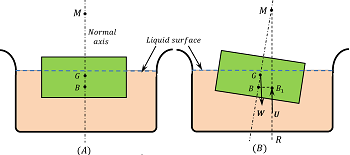
There are two conditions for equilibrium of a floating body –

Weight of the liquid displaced must be equal to the weight of the body.
The centre of gravity of the body and the centre of buoyancy must lie on the same vertical line.

Stability of floating bodies

Stability of floating body depends upon –

Weight of the body.
Weight of the displaced liquid by the body.
Position of metacentre and metacentric height.

Consider about a body floating in a liquid as shown in figure.

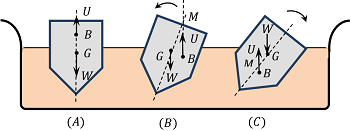
Let, the body is slightly tilted from its equilibrium position. Then, centre of body and the centre of buoyancy do not lie on the same vertical line and the weight $( W )$ of the body and up thrust $( U )$ will form a couple having rotating tendency. Three conditions are possible as follows –

Stable equilibrium

Condition for stable equilibrium is shown in figure ( B ). Here, Metacentre point $( M )$ lies above the point of centre of gravity $( G )$ .

On giving a small tilt to the floating body, the weight of the body $( W )$ and the up thrust $( U )$ will form a Righting couple.
This righting couple or restoring couple will bring the body back to its equilibrium position.
So, the body is said to be in stable equilibrium.

Unstable equilibrium

Condition for unstable equilibrium is shown in figure ( C ). Here, Metacentre point $( M )$ lies below the point of centre of gravity $( G )$ .

On giving a small tilt to the floating body, the weight of the body $( W )$ and the up thrust $( U )$ will make the body tilt further and the body will not be restored to its earlier position.
So, the body is said to be in Unstable equilibrium.

Neutral equilibrium

In this case, Metacentre point $( M )$ lies just at the point of centre of gravity $( G )$ . When the metacentre and the centre of gravity coincides, the body will remain in equilibrium in any position in which it is floating. This happens with spherical shaped bodies.

If the body is tilted, it will remain in equilibrium in the new position.
In the new position also the weight of the body $( W )$ and the up thrust $( U )$ will remain in the same position as before.
So, a body floating in this way is said to be in Neutral equilibrium.

Methods to find Metacentric height

Metacentric height of a floating body can be determined by two ways –

By analytical method.
By experimental method.

To find Metacentric height by analytics

The position of metacentre, $( M )$ with respect to the position of the centre of buoyancy $( B )$ can be determined by analytical method as follows.

Consider about a cubical body floating as shown in figure ( A ).

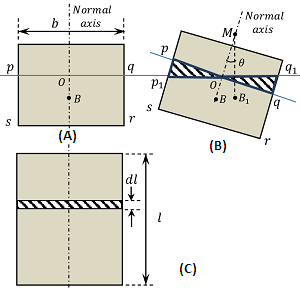
130803 FINDING METACENTRIC HEIGHT BY ANALYTICS

Let, the body is tilted by a small angle $( \theta )$ in a clockwise direction as shown in figure (B).

The immersed section has now changed from $( pqrs ) \ \text {to} \ ( p_1q_1rs )$ . Consequently, the centre of buoyancy $( B )$ has shifted to $( B_1 )$ .

The effect of tilting is to move an immersed wedge of water $( pop_1 )$ to the position $( qoq_1 )$ . This apparent movement of the water wedge has resulted in shifting the centre of buoyancy from $( B ) \ to \ ( B_1 )$ .

Since, the volume of water displaced by the floating body has not changed, we have –

$\text {Area} \ ( pop_1 ) = \text {Area} \ ( qoq_1 )$

Now let, the length of the body is $( l )$ . Consider a thin transverse section of length $( dl )$ as shown in figure ( C ).

Let –

$( b )$ is breadth of the floating body.
$( V )$ is volume of water displaced by the immersed part of body also called wetted volume.
$( dV )$ is volume of water displaced by the slice, i.e., volume of water displaced by $dl$ length of the body.
$( I )$ is moment of inertia of a horizontal section of the body at water surface about the longitudinal axis.
$( dI )$ is moment of inertia of the slice section considered about the longitudinal axis.
$( g )$ is centre of gravity of the triangular prism $( pop_1 )$ .
$( g_1 )$ is centre of gravity of the triangular prism $( qoq_1 )$ .
$( w )$ is specific weight of water.

Then, by geometry of figure –

$( g g_1 ) = \left ( \frac {2}{3} \right ) b$

Also, by Archemede’s principle –

$\text {Weight of body} = \text {Weight of water displaced by the immersed volume of body} = w V$

Again –

Weight of the slice of length $\quad ( dl = w dV )$
Volume of the triangular wedge is $\quad \left ( \frac {1}{2} \right ) \times \frac {b}{2} \times \theta dl \left ( \frac {b}{2} \right ) = \frac {b^2}{8} \theta dl$
Therefore, weight of triangular wedge is $\quad \left ( \frac {w b^2 \theta dl}{8} \right )$

Let, $( M )$ is the metacentre. Taking moments about point $( M )$ , we get –

$\text {Moment due to moving the centre of gravity of triangular prism of water from} \ g \ \text {to} \ g_1 = \text {Moment due to moving the centre of up thrust of water from} \ B \ \text {to} \ \ B_1$ .

Therefore, $\quad \left ( \frac {w b^2 \theta dl}{8} \right ) \left ( \frac {2 b}{3} \right ) = ( w dV ) ( BB_1 )$

Or, $\quad w \left ( \frac {dl b^3}{12} \right ) \theta = w dV . BB_1$

Since, $( \theta )$ is small so, $\quad BB_1 = BM \theta$

Therefore, $\quad w \left ( \frac {dl b^3}{12} \right ) \theta = w dV . BM . \theta$

But, $\quad \left ( \frac {dl b^3}{12} \right ) = dI$

Therefore, $\quad w \left ( dI \right ) \theta = w dV . BM . \theta$

Or, $\quad dI = BM . dV$

Above relation holds good for each slice of the floating body. Hence, integrating for the whole length of the body, we will get –

$I = BM V$

Therefore, $\quad BM = \left ( \frac {I}{V} \right )$

Thus, metacentric height $\quad MG = ( BM - BG )$

In this way metacentric height of a floating body can be determined analytically.

To Find Metacentric height by experiment

The position of metacentre, $( M )$ with respect to the position of the centre of buoyancy $( B )$ can be determined by experiment as follows.

Consider about the figure of a floating ship.

A small known weight $( w )$ is placed on one side of the ship.

130804 FINDING METACENTRIC HEIGHT BY EXPERIMENT
A simple pendulum is made consisting of a heavy weight $( W )$ suspended by a long cord. Pendulum is placed in the ship at a suitable location.
The position of the bob of the pendulum is marked and noted.

Let, $( l )$ is the length of the simple pendulum. Now, the weight $( w )$ is made to move from the position A to the position B as shown in figure.

Let, this displacement is $( x )$ . Since the string of the pendulum will remain plumb, the angle of heel $( \theta )$ can be measured by the apparent deflection of the pendulum.

Let, the apparent horizontal displacement of the bob of the pendulum is $( GG' = y )$ .

Then, $\quad \tan \theta = \left ( \frac {y}{l} \right )$

The moment caused by the weight of the bob equals to the moment caused by moving $( w )$ from A to B. Now, taking moments about the point $( M )$ –

Moment caused by weight of bob is $\quad ( W \times GG' ) = ( W y ) = ( W GM \tan \theta )$
Moment caused due to shifting of weight from A to B is $\quad ( w x )$

Therefore, for equilibrium we have –

$W GM \tan \theta = w x$

Therefore, Metacentric height will be –

$GM = \left ( \frac {w x}{W \tan \theta} \right )$

By knowing the values of $( w ), \ ( W ), \ ( x ) \ \& \ ( \theta )$ the value of metacentric height is calculated from above relation.

See numerical problems based on this article.