What is called a “Simple Harmonic Motion”?
A periodic oscillatory motion in which a particle moves to and fro about a mean position under the action of a restoring force which is directly proportional to its displacement from the mean position and is always directed towards the mean position, is called Simple Harmonic Motion.
A simple harmonic motion possess following characteristics –
- It should be a “to and fro” type of vibratory motion.
- Restoring force must be proportional to the displacement of particle from mean position.
- Restoring force must be acting in a direction opposite to the direction of displacement.
General conditions of Simple Harmonic Motion
A simple harmonic motion is an oscillatory motion. General condition of an oscillatory motion is given by –
F = - k x ^ n
Where, ( n ) is any odd number ( 1, 3, 5, ....... ) etc. and ( x ) is the displacement of particle from mean position.
The simplest form of oscillatory motion is a simple harmonic motion for which ( n = 1 ) .
Therefore, for a simple harmonic motion, we have –
F = - k x^{1} = - k x
In this equation, following points should be noted –
- Minus ( – ) sign indicates that, restoring force ( F ) always acts in a direction opposite to the direction of undergoing displacement ( x ) .
- Quantity ( k ) is a positive constant called force constant or spring factor.
Therefore, \quad \text {Restoring force in simple harmonic motion} \ \propto \ \text {Displacement of particle}
If, ( m ) and ( a ) are the mass and acceleration of a particle in linear motion, then from Newton’s second law of motion, we have –
F = m a
Therefore, \quad m a = - k x
Or, \quad a = - x \left ( \frac { k }{ m } \right )
But mass ( m ) and force constant ( k ) are constant for a given oscillating system.
Therefore, \quad a \propto x
Thus, a simple harmonic motion may also be defined in a different way as follows –
If a particle moves to and fro about a mean position under an acceleration which is directly proportional to displacement of particle from the mean position and is always directed towards that mean position, then its motion is called a simple harmonic motion.
EXAMPLES –
- Oscillations of loaded springs.
- Vibrations of tuning forks.
- Oscillations of a freely suspended magnet in an uniform magnetic field.
Oscillatory Motion
If a particle moves to and fro repeatedly about its mean position then its motion is called oscillatory motion or vibratory motion or harmonic motion.
An oscillatory motion has following characteristics –
- Oscillatory motion repeats again and again about a mean position i.e. at ( x = 0 ) .
- Motion remains confined within extreme positions ( x = \pm A ) .
- A force ( F ) is always acting on the particle which tries to bring the particle in its mean position. This force is called restoring force.
If, displacement of the particle is reckoned from its mean position, then –
F = - k x ^ n
Where, ( x ) is the displacement of particle from mean position and ( n ) is any odd number 1, 3, 5, ......... etc.
EXAMPLE –
- Swinging motion of pendulum of a wall clock.
- Motion of a piston of automobile engine.
- Vibrations of string of a guitar.
- Oscillations of a mass body suspended from a coil spring.
Oscillatory motion is of two types –
- Periodic motion – which repeats at regular intervals of time.
- Non-periodic motion – which repeats at irregular intervals of time.
Periodic Motion
A motion which repeats again and again at regular intervals of time is called a periodic or harmonic motion.
In nature, all types of oscillatory motions are periodic motion. But due to the presence of damping forces offered by medium particles, the amplitude of oscillations dies out with time and thus it becomes a non-periodic motion.
A periodic motion can be of the following types –
- To and fro vibratory motion in a straight line.
- A uniform circular motion.
- A uniform elliptical motion.
EXAMPLE –
- The motion of planets around the sun.
- Motion of moon around the earth.
- Motion of hands of a clock.
- Heart beat of human.
TO BE NOTED –
All oscillatory motions are periodic motions because they repeat their cycle after fixed time intervals. But it is not necessary that, all periodic motions will also be oscillatory motions.
Reason – Oscillatory motion is a “to and fro” type of vibratory motion undergoing in a straight line. But a periodic motion can be a “to and fro” type vibratory motion or a circulatory motion. A circular motion is a periodic motion but it is not an oscillatory motion.
Uniform Circular Motion is a Simple Harmonic Motion
When a particle executes an uniform circular motion, the foot of its projection on a fixed diameter executes a simple harmonic motion.
Consider about the figure shown. A particle is moving anti-clockwise direction with uniform angular velocity ( \omega ) in a circle of radius ( A ) .
When the particle or point ( P ) moves round the circumference of circle, its projection ( P' ) will execute a “to and fro” motion along a fixed diameter ( XX' ) .
PROOF –
The particle has a centripetal acceleration ( a _{ c } ) acting along the radius towards the centre O which keeps the particle moving in circular path.
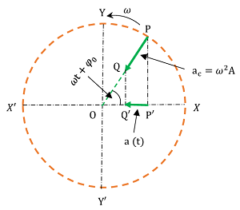
Magnitude of this centripetal acceleration will be –
a _ { c } = \omega ^2 A
Let, PQ represents the centripetal acceleration ( a _ { c } ) . Perpendicular PP' and QQ' are drawn from points P \ \text {and} \ Q respectively on diameter XX' . Then P'Q' will represent the projection of acceleration ( a _ { c } ) on fixed diameter XX' .
From geometry of the figure, we have –
- OP' = OP \cos ( \omega t + \phi _ { 0 } )
- OQ' = OQ \cos ( \omega t + \phi _ { 0 } )
Instantaneous Acceleration
Therefore, instantaneous acceleration of point P' moving on straight path XX' will be ( a _ { t } )
Acceleration of particle P' at any instant ( t ) will be the projection of the acceleration ( a _ { c } ) on XX' .
In the figure, P'Q' represents the instantaneous acceleration ( a _ { t } ) of point P' .
Therefore, \quad ( a _ { t } ) = P'Q' = ( OP' - OQ' )
= [ OP \cos ( \omega t + \phi _ { 0 } ) - OQ \cos ( \omega t + \phi _ { 0 } ) ]
= [ ( O P - O Q ) \cos ( \omega t + \phi _ { 0 } ) ]
= - a _ { c } \cos ( \omega t + \phi _ { 0 } )
= - \omega ^ 2 A \cos ( \omega t + \phi _ { 0 } ) = - \omega ^ 2 x
Therefore \quad ( a _ { t } ) = - ( \omega ^2 ) x
From above equations, it is clear that the motion of point P' has following characteristics –
- It is moving “to & fro” along fixed diameter XX' .
- Acceleration ( a _ { t } ) is proportional to the displacement ( x ) .
- Acceleration ( a _ { t } ) is acting in a direction opposite to the direction of displacement ( x ) .
These characteristics are similar to the characteristics of a Simple Harmonic Motion. Hence, the motion of point P' is a simple harmonic motion.
See numerical problems based on this article.
