What is Deflection of a beam?
When a beam or other structural member is loaded in such a way that, it is subjected to a bending moment, then due to bending stress, part of member displaces from its original position and bends downwards. Downward shifting of a beam in such a way is called deflection.
Therefore, deflection is a term used to express the degree of displacement of a beam or structural member from its original position. Practically, beams are loaded in such a way that bending moment and bending stress become the root cause of their failure. But other types of stresses are also develop in beam sections that should also be taken in consideration.
Therefore, designing of a beam section involves following strategies –
- Considerations in beam designing.
- Assumptions in beam designing.
Consideration in designing of beams
Designing of beam is based upon two main considerations. These are –
- Strength of beam – A beam should be sufficiently strong to resist developed stresses due to bending moments and shear forces. The strength of beam depends on the product of (1) Modulus of elasticity ( E ) of beam material and (2) Moment of inertia ( I ) of beam section.
- Stiffness of beam – A beam should be sufficiently stiff to resist deflection and permanent deformation which may occur beyond a permissible limit of stress. It is the degree of measurement of slope ( i ) and deflection ( y ) .
Assumptions in designing of beams
Designing of a beam is based upon two main assumptions –
- Effect of shear stress – Effect of shear stress is considered negligible during designing of a beam. But all material has its own mass and weight called self weight. This weight produces shear force and shear stress in beam section. But effect of this shear stress is very small in comparison to the bending stress. Hence to make the calculations easier, shear stress is neglected.
- Curve of bending – During designing of a beam, it is considered that the beams are bent into a circular arc. But this is not true. This will be true only in some special cases when, (1) beam is of uniform cross section (2) beam is of uniform strength (3) beam is loaded with a constant bending moment.
TO BE NOTED –
Designing of a beam of uniform cross section or uniform strength is possible but a weightless beam is not possible. Therefore, loading with constant bending moment is practically not possible due to the presence of self weight of the beam.
Equation for Deflection of beam
Consider about a beam ( AB ) which is subjected to a bending moment ( M ) . Due to this moment, beam deflects from initial position of straight line ( ACB ) to a circular arc ( ADB ) of circle ( AEB ) .
Consider about the bending of beam as shown in figure. Let –
- Length of beam is AB = ( l )
- Bending moment is ( M )
- Radius of curvature is OA = OB = ( R )
- Moment of inertia of beam section is ( I )
- Modulus of elasticity of beam material is ( E )
- Deflection of beam is CD = ( y )
- Slope of beam at ends is ( i ) as shown in figure.
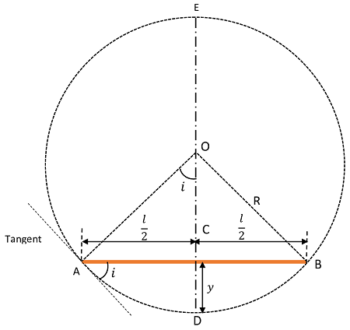
By geometry of figure, we get –
OB^2 = ( OC^2 + BC^2 ) ………. (1)
But, \quad OB = ( R ), \quad OC = \left ( OD - CD \right ) = ( R - y )
And, \quad BC = \left ( \frac {AB}{2} \right ) = \left ( \frac {l}{2} \right ) .
Thus, from equation (1), we will get –
R^2 = \left [ \left ( R - y \right )^2 + \left ( \frac {l}{2} \right )^2 \right ]
= \left [ R^2 - 2Ry + y^2 + \left ( \frac {l^2}{4} \right ) \right ]
Since, deflection of beam ( y ) is very small, so ( y^2 ) will also be very small and can be neglected. Therefore, \quad R^2 = \left [ R^2 - 2Ry + \left ( \frac {l^2}{4} \right ) \right ]
So, \quad y = \left ( \frac {l^2}{8R} \right )
Or, \quad R = \left ( \frac {l^2}{8y} \right ) ………. (2)
From, bending stress equation, we have got the relation –
\left ( \frac {M}{I} \right ) = \left ( \frac {E}{R} \right )
So, \quad R = \left ( \frac {EI}{M} \right ) ……… (3)
Substituting ( R ) from equations (2) and (3), we will get –
\left ( \frac {EI}{M} \right ) = \left ( \frac {l^2}{8y} \right )
So, \quad y = \left [ \frac {l^2}{8 \times \frac {EI}{M}} \right ] = \left ( \frac {Ml^2}{8EI} \right )
= \left ( \frac {Ml^2}{8EI} \right ) …….. (4)
This equation is called deflection equation for a beam.
From this relation, we get the magnitude of maximum deflection ( y ) at centre of a simply supported beam.
Equation for Slope of beam
From geometry of figure, we will get –
\sin i = \left ( \frac {AC}{OA} \right ) = \left ( \frac {\frac {l}{2}}{R} \right )
= \left ( \frac {l}{2R} \right ) ……. (5)
But, from relation (3) we have –
R = \left ( \frac {EI}{M} \right )
Putting the value of ( R ) in equation (5), we will get –
\sin i = \left [ \frac {l}{2 \times \left ( \frac {EI}{M} \right )} \right ]
= \left ( \frac {Ml}{2EI} \right )
Since, beam bends very slightly, hence magnitude of angle ( i ) in radians is very small.
So, \quad \left ( \sin i = i \right ) ( in radians ).
Thus, \quad i = \left ( \frac {Ml}{2EI} \right ) …….. (6)
This equation is called slope equation for a beam.
From this relation, we get maximum slope at supported ends A and B of a simply supported beam.
We will learn in detail about the procedure of application of Double integration method to find slope and deflection in beams in following numerical problems.
See numerical problems based on this article.
