Young’s Modulus of Elasticity

What is called Young’s Modulus?

When a material is axially loaded, longitudinal stress is developed in the material. Due to longitudinal stress, longitudinal strain i.e., change in length or other dimension occurs. Strain thus produced in the material body bears a constant relationship with the applied stress. This relationship is defined by Young’s modulus of elasticity.

Therefore, \quad \text {Young's modulus of elasticity} = \left ( \frac {\text {Longitudinal stress}}{\text {Longitudinal strain}} \right ) = \text {Constant}

Young’s modulus of elasticity is stated as –

“Within elastic limit, the longitudinal stress bears a constant ratio with the longitudinal strain“.

Young’s modulus of elasticity is a constant for a particular material. It is also known as Modulus of Elasticity.

Magnitude of Modulus of Elasticity

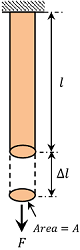
Consider about a metal wire as shown in figure. Wire is of length ( l ) and cross sectional area ( A ) is under the action of an axial pulling force ( F ) . Due to axial pull, wire undergoes an elongation ( \Delta l ) .

Then, Young’s modulus of elasticity ( E ) for the wire will be –

E = \left ( \frac {\text {Longitudinal stress}}{\text {Longitudinal strain}} \right ) = \frac {( F / A )}{( \Delta l / l )}

= \left ( \frac {F}{A} \right ) \times \left ( \frac {l}{\Delta l} \right )

Now, consider a wire whose –

• – initial length is unit i.e. ( l = 1 )
• – cross sectional area is unit i.e. ( A = 1 )
• – change in length is unit i.e. ( \Delta l = 1 )

  

Then, \quad E = \left ( \frac {F}{1} \right ) \times \left ( \frac {1}{1} \right ) = F

Therefore, Young’s modulus of elasticity of a material is the force required to extend a wire of unit length and unit area of cross section by unit amount.

Now, consider a wire of length ( l ) and unit cross section area i.e. ( A = 1 ) in which change in length is ( \Delta l = l )

Then, \quad E = \left ( \frac {F}{1} \right ) \times \left ( \frac {l}{l} \right )

Or, \quad E = F

Therefore, Young’s modulus of elasticity of a material is the axial force required to double the length of a wire of unit cross section.

Unit of Modulus of Elasticity

From definition –

Young’s modulus of elasticity is the force required to extend a wire of unit length and unit area of cross section by unit amount.

Therefore, Units of Young’s modulus of elasticity are similar to the units of stress.

• CGS unit is ( \text {dyne-cm}^{-2} ) .
• MKS unit is ( \text {kg-m}^{-2} ) .
• SI unit is ( \text {N-mm}^{-2} \ \text {or} \ \text {pascal} ) .

See numerical problems based on this article.

• P100118
• P100119

Bulk Modulus of Elasticity

Bulk modulus of elasticity is stated as –

“Within the elastic limit, the normal stress bears a constant ratio to the volumetric strain”. This ratio is called bulk modulus of elasticity.

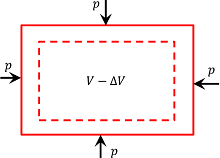
Consider about cubical body as shown in figure.

• Volume of body is ( V ) .
• Surface area is ( A ) .

Suppose, a force ( F ) acts uniformly over the whole surface and it decreases the volume by ( \Delta V ) .

Then, bulk modulus of elasticity will be –

K = \left ( \frac {\text {Normal stress}}{\text {Volumetric strain}} \right ) = - \frac {( F / A )}{( \Delta V / V )}

= - \left ( \frac {F}{A} \right ) \times \left ( \frac {V}{\Delta V} \right )

= - \left ( \frac {p V}{\Delta V} \right )

Here, \left [ p = \left ( \frac {F}{A} \right ) \right ] is the normal pressure.

Negative sign shows that, the volume decreases with the increase in stress. Units of Bulk modulus are similar to Young’s modulus.

Compressibility

The reciprocal of the bulk modulus of a material is called its compressibility.

Therefore, \quad \text {Compressibility} = \left ( \frac {1}{K} \right ) .

If the compressibility of different types of materials is compared, it is found that –

Shear Modulus of Rigidity

Shear modulus of rigidity is stated as –

“Within the elastic limit the tangential stress bears a constant ratio to shear strain”. This ratio is called modulus of rigidity.

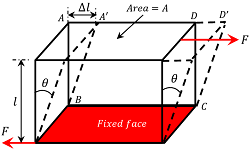
Consider a rectangular block as shown in figure.

Lower face of the block is fixed and a tangential force ( F ) is applied over its upper face of area ( A ) . An equal and opposite force ( - F ) comes into play on its lower fixed face. These two equal but opposite forces will form a couple which exerts a torque. The couple shears the block into a parallelopiped by displacing its upper face through a distance ( AA' ) = ( \Delta l )

Let, \quad AB = DC = l \quad and \quad \angle ABA' = \theta

• Then, \quad \text {Tangential stress} = \left ( \frac {F}{A} \right )
• And \quad \text {Shear strain} = \tan \theta = \left ( \frac {AA'}{AB} \right )

= \left ( \frac {\Delta l}{l} \right )

Therefore, modulus of rigidity will be –

\eta = \left ( \frac {\text {Tangential stress}}{\text {Shear strain}} \right ) = \left ( \frac {F / A}{\Delta l / l} \right )

= \left ( \frac {F}{A} \right ) \left ( \frac {l}{\Delta l} \right )

Potential energy of stretched wire

When a wire is stretched by applying a pulling force, then inter atomic force develop in wire which oppose the stretching of wire. This inter atomic force is called restoring force. Work is require to be done to overcome these restoring forces.

This work done in stretching of the wire is stored in it as its elastic potential energy.

Suppose, a force ( F ) is applied on a wire of length ( l ) which increases its length by ( \Delta l ) .

Initially the internal restoring force in the wire is zero. When wire is stretched by ( F ) , the internal force is also ( F ) .

Therefore, average internal restoring force will be –

\left ( \frac {F + 0}{2} \right ) = \left ( \frac {F}{2} \right )

Therefore, work done in stretching the wire –

W = \text {Average force} \ \times \ \text {Increase in length}

= \left ( \frac {F}{2} \right ) \times ( \Delta l ) .

This work is stored as elastic potential energy in the wire. Therefore, elastic potential energy ( U ) stored in the wire –

U = \left ( \frac {F}{2} \right ) \times ( \Delta l )

= \left ( \frac {1}{2} \right ) \left ( \frac {F}{A} \right ) \times \Delta l \times A

= \left ( \frac {1}{2} \right ) \left ( \frac {F}{A} \right ) \times \left ( \frac {\Delta l}{l} \right ) \times Al

Therefore, \quad U = \left ( \frac {1}{2} \right ) \times \ \text {Stress} \ \times \ \text {strain} \ \times \ \text {volume of wire}

Elastic energy density

Elastic potential energy per unit volume of the stretched wire is called elastic energy density.

Thus, elastic energy density is given by –

( u ) = \left ( \frac {U}{\text {Volume}} \right )

= \left ( \frac {1}{2} \right ) \times \ \text {stress} \ \times \ \text {strain}

Also, Young’s modulus \quad ( E ) = \left ( \frac {\text {Stress}}{\text {Strain}} \right )

Therefore, elastic energy density –

( u ) = \left ( \frac {1}{2} \right ) ( E \times \ \text {Strain}) \times \ \text {Strain} = \left ( \frac {1}{2} \right ) E \times \ \text {Strain}^2

Poisson’s ratio

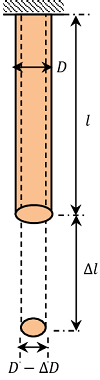
When a wire is loaded its length increases but its diameter decreases. The strain produced in the direction of applied force is called longitudinal strain. The strain produced in the perpendicular direction is called lateral strain.

Within the elastic limit, the ratio of lateral strain to the longitudinal strain is a constant for a particular material. This constant is called Poisson’s ratio.

Suppose, the length of the loaded wire increases from ( l ) to ( l + \Delta l ) and its diameter decreases from ( D ) to ( D - \Delta D ) .

Then –

• Longitudinal strain is \left ( \frac {\Delta l}{l} \right )
• Lateral strain is \left ( - \frac {\Delta D}{D} \right )

Therefore, Poisson’s ratio will be –

\sigma = \left ( \frac {\text {Lateral strain}}{\text {Longitudinal strain}} \right )

= - \left ( \frac {l}{D} \right ) \left ( \frac {\Delta D}{\Delta l} \right )

The negative sign indicates that longitudinal and lateral strains are in opposite sense.

Since the Poisson’s ratio is a ratio of two strains, it has no units and dimensions.

Other Elastic effect

Other effects due to elasticity property of a material are as follows –

Elastic After effect

Elastic bodies return to their original state on the removal of deforming force. Some bodies return to their original state immediately after the removal of the deforming force while some other bodies take a longer time to do so.

The delay in regaining the original state by a body on the removal of the deforming force is called elastic after effect.

EXAMPLE –

1. In galvanometers, Ammeters etc. suspensions are made from quartz or phosphor-bronze alloy, because their elastic after effect is small.
2. A glass fiber takes hours to regain its original state. It has a long elastic after effect.

Elastic hysteresis

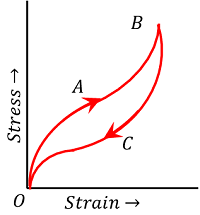
Figure shows stress-strain curve for a rubber sample when loaded and then unloaded. For increasing load, the stress-strain curve follow the path OAB and for decreasing the load, the curve follow the path BCO .

The fact that the stress-strain curve is not retraced on reversing the strain is known as elastic hysteresis.

The area under the curve OAB represents the work done per unit volume in stretching the rubber. The area under BCO represents the energy given up by rubber during unloading.

So, the area of the hysteresis loop bounded between OAB and BCO represents the energy lost as heat during the loading and unloading cycle.

Applications of elastic hysteresis –

1. Car tyres are made with synthetic rubbers having small-area of hysteresis loop so that the car tyre will not get excessively heated during the journey.
2. A padding of vulcanized rubber having large area of hysteresis loop is used in shock-absorbers between the vibrating system and the flat board. As the rubber is compressed and released during each vibration, it dissipates a large amount of vibration energy.