What is called Product of Vectors?
Multiplication of two vectors is called Product of Vectors.
Vectors have magnitude and direction both. As such, multiplication of one vector with another vector is not done by simple arithmetical or algebraic rules.
There are two distinct ways in which a vector can be multiplied by another vector. These are –
- One way of multiplication of two different vectors results in a scalar quantity and is known as scalar product. It is also termed as a dot product.
- Another way of multiplication of one vector with another vector results a new vector and is known as vector product. It is also termed as a cross product.
Scalar Product or Dot product
The scalar or dot product of two vectors ( \vec {A} ) and ( \vec {B} ) is defined as the product of the magnitudes of ( \vec {A} ) and ( \vec {B} ) and cosine of the angle ( \theta ) between them.
Therefore, \quad \vec {A} . \vec {B} = | \vec {A} | | \vec {B} | \cos \theta
= AB \cos \theta
Consider that two vectors ( \vec {A} ) and ( \vec {B} ) are represented by ( OP ) and ( OQ ) and ( \angle {POQ} = \theta ) as shown in figure.
Then, \quad \vec {A} . \vec {B} = AB \cos \theta
= A ( B \cos \theta ) = A ( OR )
= A \times Magnitude of component of \vec {B} in the direction of \vec {A} .
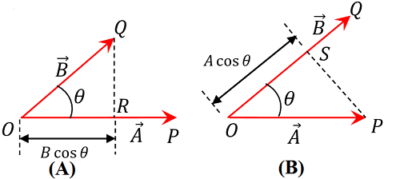
Similarly, from figure (B) we have –
\vec {A} . \vec {B} = AB \cos \theta
= B ( A \cos \theta ) = B ( OS )
= B \times Magnitude of component of \vec {A} in the direction of \vec {B} .
TO BE NOTED –
In figure (A), ( B \cos \theta ) is the projection of vector \vec {B} onto vector \vec {A} .
In figure (B), ( A \cos \theta ) is the projection of vector \vec {A} onto vector \vec {B} .
Thus, the scalar product of two vectors is equal to the product of magnitude of one vector and the magnitude of component of other vector in the direction of first vector.
EXAMPLE –
Physical examples of scalar product of two vectors are –
(1) Work done ( W ) –
It is defined as the scalar product of force vector ( \vec {F} ) acting on the body and displacement vector ( \vec {s} ) .
Thus, \quad W = \vec {F} . \vec {s}
(2) Magnetic flux ( \phi ) –
The magnetic flux linked with a surface is defined as the scalar product of magnetic field vector ( \vec B ) and the area vector ( \vec A ) .
Thus, \quad \phi = \vec B . \vec A
TO BE NOTED –
As the scalar product of two vectors is a scalar quantity, so work done and magnetic flux are all scalar quantities.
Properties of Scalar product
Scalar product of vectors has following properties –
(1) The scalar product is commutative.
Therefore, \quad \vec A . \vec B = \vec B . \vec A .
(2) The scalar product is distributive over addition.
Therefore, \quad \vec A . ( \vec B + \vec C ) = \vec A . \vec B + \vec A . \vec C .
(3) If ( \vec A ) \ \text {and} \ ( \vec B ) are two vectors perpendicular to each other, then their scalar product is zero.
Therefore, \quad \vec A . \vec B = A \ B \cos 90 \degree = 0 .
(4) If, ( \vec A ) \ \text {and} \ ( \vec B ) are two parallel vectors having same direction, then their scalar product has the maximum positive magnitude.
Therefore, \quad \vec A . \vec B = A \ B \cos 0 \degree = A B .
(5) If, ( \vec A ) and ( \vec B ) are two parallel vectors having opposite directions, then their scalar product has the maximum negative magnitude.
Therefore, \quad \vec A . \vec B = A \ B \cos 180 \degree = - A B
(6) The scalar product of a vector with itself is equal to the square of its magnitude.
Therefore, \quad \vec A . \vec A = A . A \cos 0 \degree = A . A = A^2 = | \vec A |^2 .
(7) Scalar product of two similar base vectors is unity and that of two different base vectors is zero.
Therefore, \quad \hat i . \hat i = ( 1 ) . ( 1 ) \cos 0 \degree = 1 .
Similarly, \quad \hat j . \hat j = \hat k . \hat k = 1 .
Also, \quad \hat i . \hat j = ( 1 ) . ( 1 ) \cos 90 \degree = 0 .
Similarly, \quad \hat j . \hat k = \hat k . \hat i = 0 .
(8) Scalar product of two vectors ( \vec A ) \ \text {and} \ ( \vec B ) is equal to the product of their corresponding rectangular components.
Therefore, \quad \vec A . \vec B = A_x B_x + A_y B_y + A_z B_z .
Vector Product or Cross Product
The vector product or cross product of two vectors is defined as the vector whose magnitude is equal to the product of the magnitudes of two vectors and sine of the angle between them and whose direction is perpendicular to the plane of the two vectors and is given by right hand thumb rule.
Let, ( \theta ) is the included angle between two vectors ( \vec A ) and ( \vec B ) .
Then, \quad \vec A \times \vec B = A B \sin \theta \ \hat n
Where, ( \hat n ) is a unit vector normal to the plane containing ( \vec A ) and ( \vec B ) and its direction is given by right hand thumb rule or screw rule.
Consider that, two vectors ( \vec A ) and ( \vec B ) are represented by the sides ( OP ) and ( OQ ) of a parallelogram OPRQ as shown in figure.
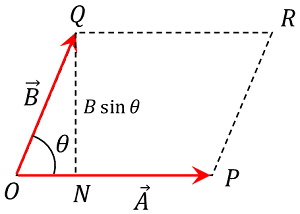
Let, ( \angle POQ = \theta )
A perpendicular QN \perp OP is drawn.
Then, magnitude of vector product will be –
| \vec A \times \vec B | = A B \sin \theta = ( OP )( OQ ) \sin \theta
= ( OP )( QN ) = Area of parallelogram OPRQ
Thus, the magnitude of the vector product of two vectors is equal to the area of the parallelogram formed by the two vectors as its adjacent sides.
Also, \quad | \vec A \times \vec B | = 2 \times \left (\frac {1}{2} \right ) ( OP )( QN )
= 2 \times Area of triangle \triangle POQ
Thus, the magnitude of the vector product of two vectors is equal to twice the area of the triangle formed by the two vectors as its adjacent sides.
Properties of Vector Product
Vector product of two vectors has following properties –
(1) The vector product is anti-commutative.
Therefore, \quad \vec A \times \vec B = - \vec B \times \vec A .
(2) The vector product is distributive over addition.
Therefore, \quad \vec A \times ( \vec B + \vec C ) = \vec A \times \vec B + \vec A \times \vec C .
(3) If, ( \vec A ) and ( \vec B ) are two vectors perpendicular to each other, then magnitude of their vector product is equal to the product of their magnitudes.
Therefore, \quad | \vec A \times \vec B | = A \ B \sin 90 \degree = AB .
(4) If, ( \vec A ) and ( \vec B ) are two parallel or anti parallel vectors, then their vector product is a zero vector.
Therefore, \quad \vec A \times \vec B = A \ B \sin ( 0 \ \text {or} \ 180 \degree ) \hat n = \vec 0 .
(5) The vector product of a vector with itself is a zero vector.
Therefore, \quad \vec A \times \vec A = A A \sin 0 \degree \hat n = \hat 0 .
(6) Vector product of orthogonal unit vectors (Base vectors).
The magnitude of each unit vectors ( \hat i ), \ ( \hat j ) and ( \hat k ) is 1 and the angle between any two of them is 90 \degree . Therefore, \quad \hat i \times \hat j = ( 1 )( 1 ) \sin 90 \degree \hat n = \hat n
As ( \hat n ) is a unit vector, normal to the plane of the unit vectors ( \hat i ) and ( \hat j ) , so it is just the third vector ( \hat k ) .
Therefore, \quad \hat i \times \hat j = \hat k
Similarly, \quad \hat j \times \hat k = \hat i
And, \quad \hat k \times \hat i = \hat j
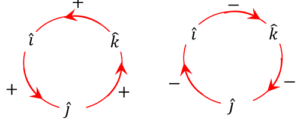
Thus, we see that, vector product of unit vectors is cyclic. Multiplying two unit vectors anticlockwise, we will get the positive value of third unit vector and by multiplying two unit vectors clockwise, we will get the negative value of third unit vector as shown in figure.
(7) The vector product of two vectors can be expressed in terms of their rectangular components as a determinant.
Therefore, \quad \vec A \times \vec B = \begin{vmatrix}\hat i & \hat j & \hat k \\ A_x & A_y & A_z \\ B_x & B_y & B_z \\ \end{vmatrix}\\
(8) Sine of the angle between two vectors.
If, ( \theta ) is the angle between two vectors ( \vec A ) \ \text {and} \ ( \vec B ) then –
| \vec A \times \vec B | = | \vec A| \ | \vec B | \sin \theta
Or, \quad \sin \theta = \frac {| \vec A \times \vec B |}{| \vec A | \ | \vec B |}
(9) Unit vector perpendicular to the plane of two vectors.
If, ( \hat n ) is a unit vector perpendicular to the plane of vectors ( \vec A ) \ \text {and} \ ( \vec B ) , then –
\vec A \times \vec B = AB \sin \theta \ \hat n = | \vec A \times \vec B | \hat n
Or, \quad \hat n = \frac { \vec A \times \vec B }{| \vec A \times \vec B |}
