Mutual Induction in Coils

How Mutual Induction in coils occur?

Mutual Induction is the phenomenon of production of induced EMF in a coil due to change in current of a near by another coil.

Consider about a coil connected to a battery. This coil is called primary coil $( P )$ . Another coil placed near the primary coil and connected to a galvanometer is called secondary coil $( S )$ as shown in figure.

When circuit is closed, battery drives a current in the primary coil and galvanometer connected to the secondary coil shows a deflection. This happens because, when the primary circuit is closed, the current through primary coil $( P )$ increases. As a result magnetic field around the coil $( P )$ increases. So, magnetic flux linked with secondary coil $( S )$ also changes.

Thus, an induced EMF is produced in the secondary coil due to the change in magnetic flux linked with it. Hence, the current flows through the secondary coil which is indicated by the deflection in the galvanometer. This phenomenon of inducing EMF is called mutual induction.

Mutual Inductance

It is seen that, the magnetic flux linked with the secondary coil $( \phi_s )$ is directly proportional to the current flowing $( I_p )$ through the primary coil.

Therefore, $\quad \phi_s \propto I_p$

Or, $\quad \phi_s = M I_p$ ……… (1)

Where $( M )$ is a constant of proportionality called Coefficient of Mutual induction or Mutual Inductance.

If, $\quad I_p = 1 \quad$ . Then, $\quad M = \phi_s$ ………. (2)

Therefore, Magnetic Inductance of two coils or circuits is defined as the magnetic flux linked with the secondary coil due to the flow of unit current in the primary coil

According to Faraday’s law of electromagnetic induction –

$\text {Induced EMF} = \text {Rate of change in linked flux}$

Therefore, $\quad \epsilon_s = - \left ( \frac {d \phi_s}{dt} \right )$

Putting the value of $( \phi_s = M I_p )$ from equation (1), we will get –

$\epsilon_s = - \frac {d ( M I_p )}{dt} = - M \left ( \frac {d I_p}{dt} \right )$

Or, $\quad \epsilon_s = - M \left ( \frac {d I_p}{dt} \right )$

Or, $\quad M = \left [ \epsilon_s / - \left ( \frac {d I_p}{dt} \right ) \right ]$

If, $\left ( - \frac {d I_p}{dt} \right ) = 1 \quad$ . Then, $\quad M = \epsilon_s$

Therefore, Mutual Inductance of two coils can also be defined as the induced EMF produced in the secondary coil due to unit rate of decrease of current in the primary coil.

Units of Mutual Inductance are same as that of units of Self Inductance.

Induction between coaxial solenoids

Consider two solenoids $( S_1 )$ and $( S_2 )$ placed co-axially such that the solenoid $( S_1 )$ completely surrounds the solenoid $( S_2 )$ .

Let, length of each solenoid is $( l )$ and the area of cross-section of each solenoid is $( A )$ . Also let, $( N_1 )$ and $( N_2 )$ are the total number of turns of respective solenoids.

092002 INDUCTION BETWEEN COAXIAL SOLENOIDS

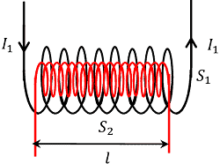
Therefore, number of turns per unit length of solenoid $( S_1 )$ will be –

$n_1 = \left ( \frac {N_1}{l} \right )$

And, number of turns per unit length of solenoid $( S_2 )$ will be –

$n_2 = \left ( \frac {N_2}{l} \right )$

Let, current $( I_1 )$ is flowing through the solenoid $( S_1 )$ .

As per Ampere’s circuital law, magnetic field in a solenoid will be –

$B = \mu_0 I$

Therefore, magnetic field of solenoid $( S_1 )$ having $( n_1 )$ number of turns will be –

$B_1 = \mu_0 n_1 I_1$

$= \mu_0 \left ( \frac {N_1}{l} \right ) I_1$

Therefore, Magnetic flux linked with each turn of solenoid $( S_2 )$ will be –

$\phi = B_1 A$

$= \mu_0 \left ( \frac {N_1}{l} \right ) I_1 A$

Then, total magnetic flux linked with $( N_2 )$ number of turns of the solenoid $( S_2 )$ will be –

$\phi_2 = \phi \times N_2$

$= \mu_0 \left ( \frac {N_1}{l} \right ) I_1 A \times N_2$

$= \left ( \frac {\mu_0 N_1 N_2 I_1 A}{l} \right )$

$= \left ( \frac {\mu_0 N_1 N_2 A}{l} \right ) I_1$ …….. (1)

Let, $( M_ {12} )$ is the mutual inductance of coil $( S_ {2} )$ due to change in magnetic field of coil $( S_ {1} )$ .

Therefore, $\quad \phi_2 = M_ {12} I_1$

Comparing it with equation (1), we will get –

$M_{12} I_1 = \left ( \frac {\mu_0 N_1 N_2 I_1 A}{l} \right ) I_1$

So, $\quad M_{12} = \left ( \frac {\mu_0 N_1 N_2 A}{l} \right )$ ……… (2)

Similarly it can be evaluated that –

$M_{21} = \left ( \frac {\mu_0 N_1 N_2 A}{l} \right )$

Here, $( M_{21} )$ is the mutual inductance of coil $( S_1 )$ with respect to the coil $( S_2 )$ .

Thus, it is seen that –

$M_{21} = M_{12} = M$ .

General form of mutual inductance is given by –

$M = \left ( \frac {\mu N_1 N_2 A}{l} \right )$

Induction between coaxial circular loops

Consider that, two co-axial circular coils or loops $C_1$ and $C_2$ of radii $( R_1 )$ and $( R_2 )$ respectively are placed apart on the same axis $OO'$ . Let $\left ( R_1 > R_2 \right )$ and the distance between the centres of the two coils is $( x )$ as shown in figure.

Let, $( I_1 )$ is the current flowing through the coil $C_1$ and $( I_2 )$ is the current through the coil $C_2$ .

According to Biot-Savart law, the magnetic field at a point on axis at a distance $( x )$ from the centre of a circular loop of radius $( R )$ carrying a current $( I )$ is given by –

$B = \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 \pi I {R}^2}{\left ( {R}^2 + x^2 \right )^{\frac {3}{2}}} \right ]$

Therefore, Magnetic field at the centre $O'$ of the coil $C_2$ due to the current in the coil $C_1$ will be –

$B_1 = \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 \pi I_1 {R_1}^2}{\left ( {R_1}^2 + x^2 \right )^{\frac {3}{2}}} \right ]$

Therefore, Magnetic flux linked with coil $C_2$ due to the magnetic field $B_1$ will be –

$\phi_2 = B_1 A_2 = \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 \pi I_1 {R_1}^2}{\left ( {R_1}^2 + x^2 \right )^{\frac {3}{2}}} \times \pi {R_2}^2 \right ]$

$= \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 {\pi}^2 I_1 {R_1}^2{R_2}^2}{\left ( {R_1}^2 + x^2 \right )^{\frac {3}{2}}} \right ]$ ……. (1)

From definition of mutual inductance, we know that –

$\text {Mutual Inductance} = \text {Flux in secondary coil due to unit current in primary coil}$

Therefore, Mutual inductance in coil $C_2$ will be –

$M_{12} = \left ( \frac {\phi_2}{I_1} \right )$

$= \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 {\pi}^2 {R_1}^2{R_2}^2}{\left ( {R_1}^2 + x^2 \right )^{\frac {3}{2}}} \right ]$

Therefore, mutual inductance between the coils will be –

$M = \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 {\pi}^2 {R_1}^2{R_2}^2}{\left ( {R_1}^2 + x^2 \right )^{\frac {3}{2}}} \right ]$ ……… (2)

Induction between concentric circular loops

Consider that, two concentric circular coils or loops $C_1$ and $C_2$ of radii $R_1$ and $R_2$ respectively $\left ( R_1 > R_2 \right )$ are placed as shown in figure.

For concentric circular loops, distance $( x )$ in equation (2) becomes zero.

Therefore putting $\left ( x = 0 \right )$ in the equation (1) we get –

Mutual Inductance $\quad M = \left ( \frac {\mu_0}{4 \pi} \right ) \left [ \frac {2 {\pi}^2 {R_1}^2}{R_2} \right ]$ …….. (3)