Screw Jack

What is a Screw Jack?

Machines are mechanical devices which are used to change the direction or magnitude of an applied force or work. A screw jack consists of two simple machines in series – (1) a lever and (2) a screw and nut assembly. A long operating handle serves as a lever whose output force turns the screw. The load is attached with the nut. So the mechanical advantage is increased by a longer handle as well as a finer screw thread.

Use of Screw Jack

Screw Jack is most popular lifting machine which uses the principle of screw and nut of a simple machine.

Screw jack is the ideal product to use for push, pull, lift, lower of heavier loads.
It is commonly used to lift moderately heavyweights, such as vehicles, to raise and lower the horizontal stabilizers of aircraft, foundations of houses and machine beds.
It is used for positioning and leveling of heavy loads like machine beds.
Screw jacks are essential components in automated machinery because of high reliability and synchronization.
Due to higher energy efficiency of screw jacks, they are used as alternatives to conventional pneumatic and hydraulic systems.

Working principle of a screw jack

Screw Jack works on the principle of working of a screw which intern uses the principle of inclined plane.

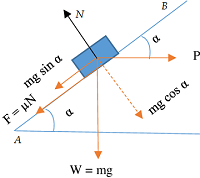
Consider about a screw jack as shown in figure. If one complete turn of a screw thread is unwound from the body of screw and flattened on a plane surface, it will form an inclined plane as shown in figure.

Let –

Pitch of thread of screw is $( p )$ .
Mean diameter of screw is $( D )$ .
Helix angle of screw is $( \alpha ) =$ Inclination of projected inclined plane.
Angle of friction for screw jack material is $( \phi )$ .

Load is kept on screw head and effort is applied on circumference of head using a long rod or lever.

For one complete rotation of screw, distance moved by effort is $\pi D$ and distance moved by load is $p$

Therefore, Velocity ratio of screw jack will be $\left ( \frac {\pi D}{p} \right )$

Considering about the figure of projected inclined plane, we have –

$\tan \alpha = \left ( \frac { p }{ \pi D } \right )$

Efficiency of a Screw Jack

Ratio of output work obtained from machine to the input work supplied to machine is called its efficiency.

Therefore, efficiency of screw jack –

$\eta = \left ( \frac {\text {Output work}}{\text {Input work}} \right )$

Efficiency can be expressed in another form as –

$\eta = \frac {\text {Ideal effort}}{\text {Actual effort}}$

Now, considering about the force of friction of screw, we find the following effects of friction –

When load is lifted the frictional force acts downward as shown in figure. Here the frictional force is acting opposite to the movement of load. Hence, total effort required to lift the load increases.
When load is being lowered the frictional force acts upward. Here the frictional force is acting in favor of direction of movement of load. Hence, total effort required to lower the load get reduced.
110802 WORKING PRINCIPLE OF A SCREW JACK

Effort required for rising of a load will be –

$P _ {Rising} = W \tan \left ( \phi + \alpha \right )$

Effort required for lowering of a load will be –

$P _ {Lowering} = W \tan \left ( \phi - \alpha \right )$

When friction is neglected, the angle of friction $( \phi )$ becomes zero.

Then ideal efficiency of screw jack for rising of a load will be –

$P_{Ideal} = W \tan \alpha$

Therefore, actual efficiency of screw jack for rising of load will be –

$\eta = \left ( \frac{\text {Ideal effort}}{\text {Actual effort}} \right )$

Or, $\quad \eta = \left [ \frac {W \tan \alpha}{W \tan (\alpha + \phi)} \right ]$

Therefore, $\quad \eta_{Rising} = \left [ \frac {\tan \alpha}{\tan (\alpha + \phi)} \right ]$

Maximum Efficiency of Screw Jack

During lifting work, expression for efficiency of a screw jack is written as –

$\eta = \left [ \frac {\tan \alpha}{\tan (\alpha + \phi)} \right ]$

$= \left [ \left ( \frac {\sin \alpha}{\cos \alpha } \right ) \div \left ( \frac {\sin ( \alpha + \phi)}{\cos ( \alpha + \phi )} \right ) \right ]$

$= \left [ \frac{ \sin \alpha \times \cos \left ( \alpha + \phi \right ) }{ \cos \alpha \times \sin \left ( \alpha + \phi \right ) } \right ]$

Multiplying numerator and denominator by $2$ , we will get –

$\eta = \left [ \frac { 2 \sin \alpha \times \cos \left ( \alpha + \phi \right ) }{ 2 \cos \alpha \times \sin \left ( \alpha + \phi \right ) } \right ]$

Using trigonometric identities, we have –

$\quad \left [ \sin ( A + B ) + \sin ( A - B ) = 2 \sin A \cos B \right ]$
$\quad \left [ \sin ( A + B ) - \sin ( A - B ) = 2 \cos A \sin B \right ]$

Therefore, efficiency of screw jack will be –

$\eta = \left [ \frac { \sin \left ( 2 \alpha + \phi \right ) - \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]$

So, $\quad \left [ \left ( 1 - \eta \right ) \right ] = \left [ 1 - \frac { \sin \left ( 2 \alpha + \phi \right ) - \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]$

$= \left [ \frac { 2 \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]$

From expression, it is clear that, efficiency of screw jack will be maximum when $\left ( 1 - \eta \right )$ will be minimum.

But for a given screw, $( \phi )$ is a constant term because it depends on material of the screw. Therefore, $\left ( 1 - \eta \right )$ will be minimum, when $[ \sin \left ( 2 \alpha + \phi \right ) ]$ is maximum.

Hence, putting the maximum possible value of $[ \sin \left ( 2 \alpha + \phi \right ) ] = 1$ in efficiency expression, we will get maximum efficiency.

Therefore, maximum efficiency for screw jack –

$\eta _ {Max} = \left [ \frac { \sin \left ( 2 \alpha + \phi \right ) - \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]$

$= \left [ \frac { 1 - \sin \phi }{ 1 + \sin \phi } \right ]$

Overhauling of Screw Jack

During lowering operation of a load, required effort $( P )$ is given by –

$P = W \tan \left ( \phi - \alpha \right )$

In the above expression, if $( \phi < \alpha )$ , then the effort required in lowering the load will be negative. In other words, the load will start moving downward without the application of any effort. Such a condition is called overhauling of a screw and the machine is called a reversible machine.

A lifting machine is called a reversible machine if it is capable of doing work in reverse direction when the applied effort is removed.

Reversibility feature is not a desirable quality for a lifting machines. When the applied effort is removed, the lifted load will lower by itself which may cause accident and damage to the equipment.

If $( \phi > \alpha )$ , then the effort required to lower the load will be positive. That means an effort is required to lower the load. Such a screw is called self locking screw.

Therefore, a lifting machine must be irreversible or self-locking.

Hence, for self locking of a screw, the friction angle $( \phi )$ is greater than helix angle $( \alpha )$ .

Let, $( P_{Actual} )$ is the actual effort required to lift a load and $( P_{Ideal} )$ is the ideal effort neglecting friction force.

Then, velocity ratio for screw jack will be –

$VR = \left ( \frac { W }{ P_ { Ideal }} \right )$

Or, $\quad ( P _ { Ideal } ) = \left ( \frac { W }{ VR } \right )$

And, effort lost in friction will be –

$( P _ { Friction } ) = ( P _ { Actual } - P _ { Ideal } ) = \left [ P _ { Actual } - \left ( \frac { W }{ VR } \right ) \right ]$

When, applied effort $( P_{Actual} )$ is removed, the force resisting the spontaneous falling down of load will be the force of friction. This force of friction is equal to $\left [ P _ { Actual } - \left ( \frac { W }{ VR } \right ) \right ]$

If this frictional force is greater than $( P_{Ideal} )$ ,then load $( W )$ will not fall spontaneously even when effort $( P_{Actual} )$ is removed.

Therefore, friction force $\left [ P _ { Actual } - \left ( \frac { W }{ VR } \right ) \right ]$ is necessary to balance the load $( W )$ in the absence of effort.

Hence, necessary condition for a machine to be irreversible or self locking is –

$( P _ { Friction } ) > ( P _ { Ideal } )$

So, $\quad ( P _ {Actual} - P _ {Ideal} ) > ( P _ {Ideal} )$

Therefore, $\quad ( P _ {Actual} ) > 2 ( P _ {Ideal} )$

Therefore, for a self locking machine actual effort required for lifting a load is more than double of the ideal effort required for lifting the same load.