What is called Gravitational Potential?
Gravitational potential at a point in the gravitational field of a body is defined as the amount of work done in bringing a body of unit mass from infinity to that point.
Therefore, gravitational potential at a point in the gravitational field is given by –
V = \left ( \frac {\text {Work done}}{\text {Mass}} \right )
Or, \quad V = \left ( \frac { W }{ m } \right )
- The gravitational potential is a scalar quantity.
Earth’s Gravitational Potential
From definition, work done in moving a particle through a distance is given by –
W = ( \text {Force} \ \times \ \text {Distance moved by body} )
Therefore, work done in bringing a body of mass ( m ) to a point at distance ( r ) from the centre of the earth will be –
W = - \left ( \frac { G M m }{ r^2 } \right ) \ \times \ r
Or, \quad W = - \left ( \frac { G M m }{ r } \right )
- Hence gravitational potential due to the earth at that point will be –
V = \left ( \frac { W }{ m } \right ) = - \left ( \frac { G M m }{ r } \right ) \ \div \ m
- Therefore, \quad V = - \left ( \frac { G M }{ r } \right )
At the surface of the earth \quad ( r = R )
- Therefore, gravitational potential at the earth’s surface will be –
V_{ surface } = - \left ( \frac { G M }{ R } \right )
Gravitational Field
Gravitational field of a body is a space surrounding that body within which its gravitational force of attraction can be felt by another body.
- Gravitational field is a natural phenomenon.
- All material bodies produce its own gravitational field around itself in concentric spherical fashion.
Intensity of Gravitational Field
Intensity of gravitational field at a point is defined as the force experienced by a body of unit mass placed at that point.
Therefore, \quad \text {Gravitational field intensity} = \left ( \frac {\text {Gravitational force}}{\text {Mass}} \right )
- Gravitational field intensity is a vector quantity and denoted by ( \vec { E } ) .
- It always acts towards the source body producing that gravitational field.
Consider about a source body of heavy mass ( M ) as shown in figure. The body will produce its gravitational field around it.
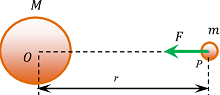
A test body of mass ( m ) is brought at point P within the gravitational field of the source body. Let, the point P is at a distance ( r ) from centre O of the source body.
- From Newton’s laws of gravitation, the test body will experience a gravitational pull of magnitude –
\vec { F } = \left ( \frac { G M m }{ r^2 } \right )
- Therefore, gravitational field intensity at point P will be –
\vec { E } = \left ( \frac { \vec { F }}{ m } \right ) ……… (i)
Or, \quad E = \left ( \frac {F}{m} \right ) = \left ( \frac { G M }{ r^2 } \right ) ……….. (ii)
At infinity, gravitational field intensity becomes zero.
Thus gravitational field intensity decreases as distance ( r ) increases and becomes zero at infinity.
- The direction of ( \vec {E} ) is same as that of ( \vec {F} )
If the test mass is free to move, it will move towards mass ( m ) with an acceleration ( a ) under the influence of force ( F ) .
Therefore, \quad a = \left ( \frac { F }{ m } \right ) …….. (iii)
From equations (ii) and (iii), we get –
a = E
Thus the intensity of gravitational field at any point is equal to the free acceleration produced in the test mass when placed at that point.
Intensity of Earth’s Gravitational Field
The gravitational field intensity of earth at any point near the earth’s surface is equal to the acceleration produced in freely falling body at that point.
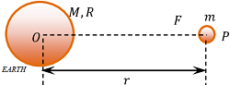
Consider about a body placed at a distance of ( r ) from the centre of the earth O as shown in figure.
- The gravitational field intensity at point P will be –
\vec { E } = \left ( \frac { \vec { F }}{ m } \right ) = \left ( \frac { G M }{ r^2 } \right )
For a point on the surface of the earth ( r = R ) .
- Therefore, \quad E_{surface} = \left ( \frac { G M }{ R^2 } \right ) = g
Gravitational Potential Energy
Gravitational potential energy of a body is the energy possessed by that body due to its position in the gravitational field of another body.
- Potential energy is the amount of work done in bringing a body from infinity to a given point in the gravitational field.
Consider about a sphere of mass ( M ) and radius ( R ) . A smaller body of mass ( m ) is located at point P such that ( OP = r ) where ( r > R ) as shown in figure.
Let, at an instant the smaller body is at A such that ( OA = x )
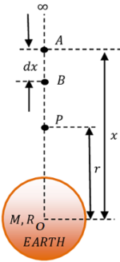
- The gravitational force on the body at will be –
F = \left ( \frac { G M m }{ x^2 } \right )
Now let, the body is moved through a small distance ( dx ) .
- The small work done in moving the body through this distance will be –
d W = F dx = \left ( \frac { G M m }{ x^2 } \right ) dx
- Then total work done in bringing the body from infinity i.e. ( x = \infty ) to the point P i.e. at ( x = r ) will be –
W = \int { d W } = \int\limits_{ \infty }^{ r } \left ( \frac { G M m }{ x^2 } \right ) dx
Or, \quad W = \left ( G M m \right ) \int\limits_{ \infty }^{ r } x^{ -2 } dx
= ( G M m ) \left [ - \frac { 1 }{ x } \right ]_{ \infty }^{ r }
= - ( G M m ) \left [ \frac { 1 }{ r } - \frac { 1 }{ \infty } \right ]
Therefore, \quad W = - \left ( \frac { G M m }{ r } \right )
- This work done is stored as the gravitational potential energy ( U ) in the body.
Therefore, \quad U = - \left ( \frac {GMm}{r} \right ) ……. (1)
TO BE NOTED –
- In above equation, negative sign indicates that work is being done on the body by the gravitational force.
- As the distance ( r ) increases, the gravitational potential energy increases.
- At ( x = \infty ) the maximum ( PE ) becomes zero.
Change in Potential Energy
Rewriting the equation for gravitational potential energy, we get –
U = - \left ( \frac { G M m }{ r } \right ) = \left ( - \frac { G M }{ r } \right ) \times m
But \quad \left ( - \frac { G M }{ r } \right ) = V ( Gravitational potential ).
Therefore, \quad U = ( V ) \times ( m )
- Hence, \text {Gravitational potential energy} = \text {Gravitational potential} \ \times \ \text {Mass}
If a body of mass ( m ) is moved from a point at distance ( r_1 ) to a point at distance ( r_2 ) then the change in (PE ) of body will be –
dU = \int\limits_{ r_1 }^{ r_2 } \left ( \frac {GM m}{ x^2 } \right ) dx
= ( G M m ) \left [ - \frac { 1 }{ x } \right ]_{ r_1 }^{ r_2 }
= ( G M m ) \left [ \frac { 1 }{ r_1 } - \frac { 1 }{ r_2 } \right ]
- Therefore, if ( r_1 > r_2 ) then ( \Delta U ) will be negative.
So when a body is brought closer to earth’s surface, its gravitational potential energy decreases.
Therefore, if ( r_1 = R ) and [ r_2 = ( R + h ) ] \quad Then \quad \Delta U = mgh
See numerical problems based on this article.
