What is called a Rolling Motion?
Rolling motion is particular type of motion in which a circular or spherical object makes a combination of rotation and translation.
For example, if a marble sphere is thrown on the floor, it is rolling on the surface of the floor. The sphere will be in the rotation motion being rotating about its own axis. At the same time, the sphere will move from one point to another point on the floor surface, so there is a translation motion too.
When a cylindrical object moves on with curved surface in contact or a circular disc moves on its circumference in contact with a flat surface, the motion is called a rolling motion.
A rolling motion is a combination of rotary motion and translation motion.
Analysis of Rolling Motion
Consider about a disc of radius R rolling on a level surface without slipping as shown in figure. The disc is rotating clockwise so as its centre of mass point C moves rightward.
Rolling motion of the disc has two simultaneous motions –
- Translation motion.
- Rotational motion.
Translation motion
Translation velocity of disc is the velocity of its centre of mass ( \vec {v_{cm}} ) .
Because, centre of mass of disc is the geometric centre C , so ( \vec {v_{cm}} ) is parallel to the level surface.
Therefore, \quad \vec {v_{trans}} = \vec {v_{cm}}
The translation velocity will be constant at ( \vec {v_{cm}} ) for each particle on the disc.
Rotational motion
The disc rotates with angular velocity ( \omega ) about its axis of rotation through C .
Consider about a particle P at a distance ( r ) from the axis of rotation.
The rotational velocity of the particle P is –
\vec {v_{rot}} = \vec r \omega
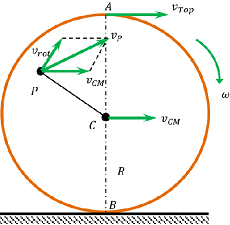
Therefore, rotational velocity ( \vec {v_{rot}} ) of a particle on the disc is always changing. It is proportional to the distance of the particle from the axis of rotation i.e. point ( C ) . Direction of this rotational velocity ( \vec {v_{rot}} ) will be perpendicular to the radius vector CP .
Therefore, effective linear velocity ( v_p ) will be the resultant of the two velocities ( \vec {v_{rot}} ) and ( \vec {v_{cm}} ) .
It is seen that, the velocity ( v_p ) is perpendicular to the line joining the contact point B and point P .
Therefore, the line passing through the bottom point B and parallel to the axis through C is called instantaneous axis of rotation.
Velocity of point of contact
Consider about the disc of radius R rolling on a level surface without slipping as shown in given figure above.
Point B is the point of contact of the disc with the surface. At this point, linear velocity due to rotation of the disc ( \vec {v_{rot}} ) is directed exactly opposite to the translation velocity ( \vec {v_{cm}} ) .
Therefore, at point B –
- Translation velocity is \quad ( \vec {v_{trans}} ) = ( \vec {v_{cm}} )
- Rotational velocity is \quad ( \vec {v_{rot}} ) = R \omega = ( - \vec {v_{cm}} )
- Both velocities are acting parallel to the level surface.
Therefore, resultant velocity of point B will be –
\vec {v_{B}} = \vec {v_{cm}} + \vec {v_{rot}}
Or, \quad \vec {v_{B}} = ( \vec {v_{cm}} ) + ( - \vec {v_{cm}} ) = 0
Therefore, the point B will be instantaneously at rest if there is no slipping.
Velocity of Top point
At the top point A of the disc –
The linear velocity ( R \omega ) due to rotational motion and the translation velocity ( \vec {v_{cm}} ) are in the same direction parallel to the level surface.
Therefore, \quad \vec {v_{top}} = R \omega + \vec {v_{cm}}
= \vec {v_{cm}} + \vec {v_{cm}} = 2 \vec {v_{cm}}
= 2 \vec {v_{cm}}
Kinetic energy of Rolling motion
The kinetic energy of a body which is in rolling motion without slipping is the sum of kinetic energies of translation motion and rotation motion.
Therefore, \quad \text {Energy of Rolling motion} = \text {KE of Translation motion of centre of mass} + \text {KE of Rotational motion about centre of mass}
Or, \quad \text {Energy of Rolling motion} = \left ( \frac {1}{2} \right ) m ( v_{cm} )^2 + \left ( \frac {1}{2} \right ) I ( \omega )^2
But, \quad v_{cm} = R \omega \quad and \quad I = m k^2
Therefore, \quad \text {Energy of Rolling motion} = \left ( \frac {1}{2} \right ) m ( v_{cm} )^2 \left [ 1 + \left ( \frac {k^2}{R^2} \right ) \right ]
