Organ Pipe Vibrations

What is an Organ Pipe?

An organ pipe is the simplest musical instrument in which sound is produced by setting an air column into vibrations.

Organ pipes are of two types –

Open organ pipe – If both the ends of an organ pipe are open then it is called an open organ pipe. Open end of the pipe behaves as an open boundary.
Closed organ pipe – If one end of an organ pipe is closed then it is called a closed organ pipe. Closed end of the pipe behaves as a rigid boundary.

Open Organ Pipe

Construction of an open organ pipe is shown in figure.

When air is blown into the open organ pipe through the mouth piece $( M )$ , it strikes against the slanting surface $( B )$ and deflected upwards. Air issues out of the slit $( S )$ in the form of a jet. This jet of air strikes to the sharp edge called lip $( L )$ , which is now set into vibrations. This produces a sound called edge tone. The frequency of edge tone depends upon the pressure of the air stream inside the organ pipe. The sound waves travel down the pipe and get reflected at its open end producing longitudinal stationary waves. If the frequency of these reflected waves is equal to the frequency of the edge tone then resonance occurs and a loud sound is produced.

As both ends of the pipe are open so reflection of waves from open end occur from the open end without any phase change. However, the particles continue to move in the same direction even after the reflection of waves.

The displacement of particles is maximum at the open end i.e. anti-node is formed at the open end.

TO BE NOTED –

Reflection of Sound Waves –

When progressive waves strikes an open or flexible boundary ( diaphragm or open atmosphere etc. ), they get reflected on same path without any phase difference. Only the direction is reversed. Hence, an anti-node is formed at the boundary interface.
When progressive waves strikes a rigid boundary ( closed end of pipe, wall etc. ), they get reflected on same path with a phase difference of $( \pi )$ radians. Hence, a node is formed at the boundary interface.

First Mode of vibrations

Both ends of an open organ pipe are open. Let, the length of the pipe is $( L )$ . In the simplest form of vibrations there is one node in the middle and two anti-nodes at the ends of the pipe as shown in figure. Let, the wavelength of setup vibration is $( \lambda_1 )$

OPEN ORGAN PIPE - FIRST MODE VIBRATION — 061902 OPEN ORGAN PIPE – FIRST MODE VIBRATION

Entire length of the pipe is divided into two sections of length $\left ( \frac {\lambda_1}{4} \right )$

Therefore, $\quad L = 2 \left ( \frac { \lambda _ 1 }{ 4 } \right ) = \left ( \frac { \lambda _1 }{ 2 } \right )$

Or, $\quad \lambda _ 1 = 2 L$

Frequency of a vibration is given by $\left [ \nu = \left ( \frac { v }{ \lambda } \right ) \right ]$ and velocity of sound in air is $\left [ v = \sqrt { \frac { \gamma P }{ \rho }} \right ]$

Therefore, frequency of first mode of vibrations will be –

$\nu _ 1 = \left ( \frac { v }{ \lambda _ 1 } \right ) = \left ( \frac { 1 }{ 2 L } \right ) \left ( \sqrt { \frac { \gamma P }{ \rho }} \right )$

This frequency is called fundamental frequency or first harmonic frequency.

Second Mode of vibrations

In second mode of vibrations, anti-nodes at the open ends are separated by two nodes and one anti-node as shown in figure. Let, the wavelength of setup vibration is $( \lambda_2 )$

OPEN ORGAN PIPE - SECOND MODE VIBRATION — 061903 OPEN ORGAN PIPE – SECOND MODE VIBRATION

Entire length of the pipe is divided into four sections of length $\left ( \frac {\lambda_2}{4} \right )$

Therefore, $\quad L = 4 \left ( \frac { \lambda _ 2 }{ 4 } \right ) = \lambda _ 2$

Or, $\quad \lambda _ 2 = L$

Therefore, frequency of second mode of vibrations will be –

$\nu _ 2 = \left ( \frac { v }{ \lambda _ 2 } \right ) = \left ( \frac { 1 }{ L } \right ) \left ( \sqrt { \frac { \gamma P }{ \rho }} \right )$

$= 2 \left [ \left ( \frac { 1 }{ 2L } \right ) \left ( \sqrt { \frac { \gamma P }{ \rho }} \right ) \right ]$

Therefore, $\quad \nu_2 = 2 \nu_1$

This frequency is called first overtone frequency or second harmonic frequency.

Third Mode of vibrations

In third mode of vibrations, anti-nodes at the open ends are separated by three nodes and two anti-nodes as shown in figure. Let, the wavelength of setup vibration is $( \lambda_3 )$

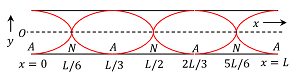
OPEN ORGAN PIPE - THIRD MODE VIBRATION — 061904 OPEN ORGAN PIPE – THIRD MODE VIBRATION

Entire length of the pipe is divided into six sections of length $\left ( \frac {\lambda_3}{4} \right )$

Therefore, $\quad L = 6 \left ( \frac { \lambda _ 3 }{ 4 } \right )$

Or, $\quad \lambda _ 3 = \left ( \frac { 2 L }{ 3 } \right )$

Therefore, frequency of third mode of vibrations will be –

$\nu _ 3 = \left ( \frac { v }{ \lambda _ 3 } \right ) = \left ( \frac { 3 }{ 2 L } \right ) \left ( \sqrt { \frac { \gamma P }{ \rho }} \right )$

$= 3 \left [ \left ( \frac { 1 }{ 2L } \right ) \left ( \sqrt { \frac { \gamma P }{ \rho }} \right ) \right ]$

Therefore, $\quad \nu_3 = 3 \nu_1$

This frequency is called second overtone frequency or third harmonic frequency.

We see that, various frequencies of an open organ pipe are in the ratio of $( 1 : 2 : 3 : 4 \ .... )$ and so on. These are called harmonics.

Therefore, in an open organ pipe, harmonics are integral multiples of fundamental frequency.