What is called Moment of Inertia?
All material bodies possess a unique property by virtue of which they resist to change in their state of rest or motion by itself. This property of material body is known as inertia. Similarly, the property of a material body by virtue of which it resists to change in its state of motion along a circular path or curve or rotary motion, is called Inertia of moment or Moment of inertia.
Moment of inertia of a body comes into action and resist the changes in motion in following cases –
- If the body is moving in circular motion or in curved path.
- If the body is rotating or revolving about an axis.
Moment of inertia is also known as Second Moment or Moment of Moment. In short form, moment of inertia is written as MI.
Types of Moment of Inertia
Basically, moment of inertia of an object can be in three forms –
1) Force moment of inertia –
It is the moment of moment of a force.
- Its magnitude is given by \left ( F x^2 \right ) .
- Here ( F ) is the magnitude of force and ( x ) is the distance of line of action of this force from the axis of rotation.
2) Area moment of inertia –
It is the moment of an area.
- Its magnitude is given by \left ( A x^2 \right ) .
- Here ( A ) is the area of two dimensional object like a lamina and ( x ) is the distance of geometrical centroid of area from the axis of rotation.
3) Mass moment of inertia –
It is the moment of a mass.
- Its magnitude is given by \left ( M x^2 \right ) .
- Here ( M ) is the mass of a body and ( x ) is the distance of centre of gravity of the body from the axis of rotation.
See numerical problems based on this article.
Radius of gyration
Radius of gyration of a body is defined as the radius of an imaginary circular ring whose mass is equal to the mass of that body.
Consider about a body of mass ( M ) which is rotating about an axis. The body may be considered to be composed of numerous particles of small masses ( m_1, \ m_2 \ ..... \ m_n ) etc.
Hence, the mass of body will be ( M ) = ( m_1 + m_2 + ........ + m_n ) = \left ( \sum {m} \right ) . Let, the distances of these small masses from the axis of rotation, are ( r_1, \ r_2 \ ...... \ r_n ) etc. So, moments of these mass particles about the axis of rotation will be –
m_1 r_1^2, \quad m_2 r_2^2 \quad ......... \quad m_n r_n^2 \quad etc.
Therefore, moment of inertia of whole body will be –
MI = ( m_1 r_1^2 + \ m_2 r_2^2 + ........ + \ m_n r_n^2 )
= \left ( \sum {mr}^2 \right )
Let, ( MI ) of the body is equivalent to the ( MI ) of a circular ring whose mass is equal to the mass ( M ) of body and radius is ( k ) .
Therefore, \quad MI = ( M \ k^2 ) . Here, ( k ) is called radius of gyration of body. It is also called swing radius.
So, \quad k = \sqrt { \frac { \sum {m \ r}^2 }{ M } } .
Similarly, for area moment of inertia, radius of gyration \quad k = \sqrt { \frac { \sum {a \ r}^2 }{ A } } . Where, total area \quad A = ( a_1 + a_2 + ....... + a_n ) = \sum a .
Routh’s Rule
Routh’s rule is a thumb rule to find the moment of inertia of three dimensional symmetrical solid objects.
Routh rule is not valid for two dimensional objects, such as lamina etc. It is applicable for bodies which satisfy the following conditions –
- Object should be a three dimensional solid object.
- Routh rule is applicable for objects which are symmetrical in all the three axes i.e. X axis, Y axis and Z axis.
- So, it is applicable for circular or elliptical cylinders, cuboid, circular disc etc. rotating about any axis of symmetry.
Routh’s rule states that –
(1) Area Moment of Inertia – For an object of area ( A ) , moment of inertia about an axis will be –
MI = A \left [ \frac {\text {Sum of squares of perpendicular axes}}{3, \ 4 \ or \ 5} \right ]
(2) Mass moment of inertia – For an object of mass ( M ) , moment of inertia about an axis will be –
MI = M \left [ \frac {\text {Sum of squares of perpendicular axes}}{3, \ 4 \ or \ 5} \right ]
In above expressions, ( 3, \ 4, \text {and} \ 5 ) are the numbers which depends on the shapes of that object. It is –
- Three ( 3 ) for a rectangular or square body or lamina.
- Four ( 4 ) for a circular or elliptical body or lamina.
- Five ( 5 ) for spherical or ellipsoidal body.
ILLUSTRATION
Consider about an elliptical lamina as shown in figure.
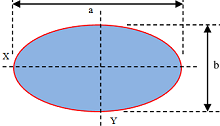
For this object the axes are ( a ) and ( b ) in X and Y directions respectively.
Therefore, sum of the axes is \left ( a^2 + b^2 \right ) and in the denominator we use ( 4 ) (for an elliptical lamina).
Therefore, by Routh’s rule the area moment of inertia of the elliptical lamina will be –
MI_Z = A \left ( \frac { a^2 + b^2 }{ 4 } \right )
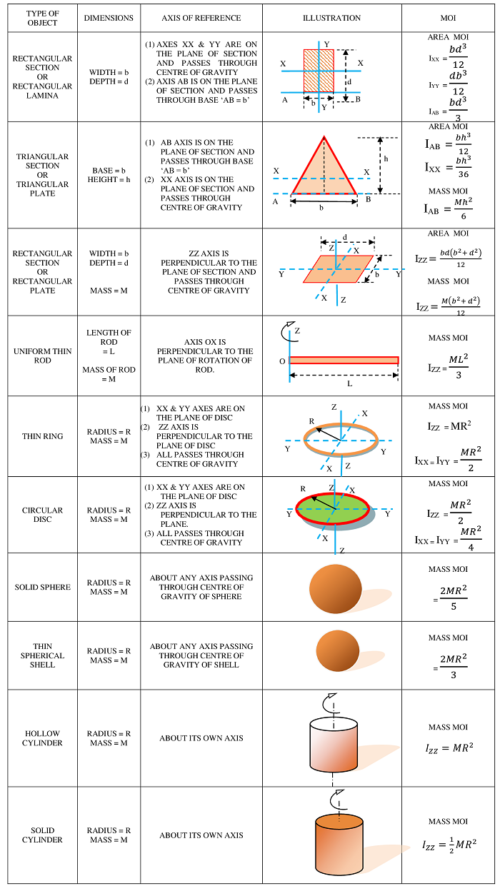
Moment of Inertia of common objects
Moment of inertia for simple geometrical shapes about different axes is given below. It is very helpful in comparing of values of moments of inertia between similar objects.
Steps to find Moment of Inertia
To find ( MI ) of an irregular shaped object, we use integration method. It involves following steps –
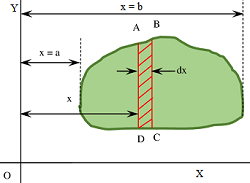
STEP 1 – DRAW A SKETCH AND CO-ORDINATE AXES
- Draw a neat sketch of the object as shown in figure. A rough sketch without any scale is sufficient for this purpose.
- Draw the reference axes X axis and Y axis and origin O .
STEP 2 – CUT AN ELEMENTARY STRIP
- Imagine two cutting planes parallel to YY' axis passing through distances of ( x ) and ( x + dx ) .
- Thus, an elementary strip ABCD is cut out as shown in figure as shaded area.

101103 INTEGRATION METHOD FOR MOMENT OF INERTIA OF SOLIDS
Width of the elementary strip will be ( dx ) . Let, length of this strip is ( L ) .
Since the cutting planes are very close, so strip area ABCD can be considered as a perfect rectangle. Therefore, area of elementary strip dA = ( L \times dx ) .
In this equation, length ( L ) is a variable which varies with distance ( x ) of cutting planes from YY' axis.
Now, using geometric and trigonometric relations, we can express the length of elementary strip in terms of variable ( x ) .
STEP 3 – FIND CENTRE OF GRAVITY AND MOMENT OF INERTIA FOR ELEMENTARY STRIP
Centre of gravity of elementary strip will be at a distance of \left ( x + \frac {dx}{2} \right ) from YY' axis. But ( dx ) is very small. Hence \left ( \frac {dx}{2} \right ) can be neglected.
( MI ) of elementary strip about YY' axis will be –
dM = ( dA \ x ) x = x^2 \ dA = x^2 \ L \ dx
STEP 4 – DIVIDE WHOLE OBJECT INTO NUMEROUS STRIPS
Using similar parallel cutting planes, the whole object is assumed to cut into several elementary strips. Distance ( x ) for these cutting planes will be different for different strips. It varies from ( x = a ) to ( x = b ) . Therefore, ( MI ) for elementary strips will be –
dM_1 = ( x_1 )^2 dA_1, \quad dM_2 = ( x_2 )^2 dA_2 \quad .... etc. Here, ( dA_1 ), \ ( dA_2 ) \ ...... etc. are the area of different elementary strips.
STEP 5 – APPLY INTEGRATION METHOD
Total ( MI ) of the object will be the sum of elementary moment of inertia for each strip. Therefore, \quad MI = ( dM_1 + dM_2 + \ .... + dM_n )
= \sum {dM}
= \sum_{a}^{b} x^2 \ dA
Now by applying integration method, we get –
MI_{yy} = \int\limits_{b}^{a} x^2 \ dA
Integrating above expression, we will get ( MI ) of the whole object about YY' axis.
Similarly, repeating steps from 1 to 5 , ( MI ) for the object about XX axis can be obtained.
See numerical problems based on this article.