Capillarity

What is cslled capillarity?

Capillarity is the phenomenon of rising or dipping of liquid surface in a narrow tube when it is dipped in the liquid.

• Capillarity is caused due to the properties of adhesion and cohesion.

The surface of liquid in the capillary tube is called meniscus.

1. If the liquid wets the tube ( i.e. adhesion is predominant ) the meniscus is concave upward and the liquid level rises in the tube.
2. If the liquid does not wet the tube ( i.e. cohesion is predominant ) the meniscus is convex upward and the liquid level falls in the tube.

Angle of contact

Angle ( \theta ) made by the tangent to the liquid surface at the point of contact and the wall of the tube is called angle of contact.

The value of angle of contact depends upon the following factors –

1. Nature of the solid surface and the liquid in contact.
2. Cleanliness of the surface in contact.
3. Medium above the free surface of the liquid.
4. Temperature of the liquid.

The liquid surface is usually curved when it is in contact with a solid surface. This is called meniscus. The shape which the liquid surface takes depends upon the relative strengths of cohesive and adhesive forces.

1. If \text {adhesive force} > \text {Cohesive force} – Liquid wets the solid surface. The angle of contact is acute and the liquid surface has a concave meniscus.
2. If \text {adhesive force} < \text {Cohesive force} – Liquid does not wet the solid surface. The angle of contact is obtuse and liquid surface has a convex meniscus.
3. If \text {adhesive force} = \text {Cohesive force} – Liquid surface is plane. The angle of contact is a right angle.

• The above phenomenon is known as capillarity.

Capillary Tube

A narrow glass tube of small diameter which is open at both ends is called a capillary tube.

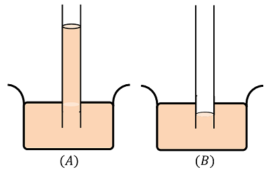
• When a capillary tube is dipped into a liquid like water, we find that the liquid rises in the tube above the general level of the outside liquid as shown in figure ( A ).
• But, if the same glass tube is dipped in a heavy liquid like mercury, the level of the liquid in the tube is lower than the general level of the outside liquid as shown in figure ( B ).

Ascent formula of capillary rise

Consider about the figure (A) for the capillary rise of a liquid in a tube of radius ( r ) . Let, the rise of the liquid in the tube is ( h ) .

Let, ( \sigma ) is the surface tension of the liquid and ( \theta ) is the angle of contact between the liquid and the glass tube.

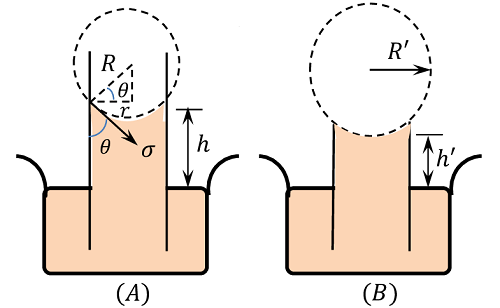
Then, weight of the column of liquid of height ( h ) in the tube is balanced by the vertical component of the surface tensile force.

• Vertical component of the surface tension force is –

\sigma \times ( 2 \pi r ) \cos \theta

• Weight of the column of liquid in capillary tube is –

\pi r^2 h \rho g

Therefore, for equilibrium of the liquid column in tube –

\sigma \times ( 2 \pi r ) \cos \theta = \pi r^2 h \rho g

Or, \quad h = \left ( \frac {2 \sigma \cos \theta}{\rho g r} \right )

• This is called Ascent formula for rise of liquid in a capillary tube.

Also, \quad h = \left ( \frac {4 \sigma \cos \theta}{\rho g d} \right )

Where ( d = 2r ) is the diameter of the tube.

• \theta = 25 \degree 32' \text {for water, and} 128 \degree 52' for mercury.

The ascent formula shows that the height ( h ) to which a liquid rises in the capillary tube is –

1. – inversely proportional to the radius of the tube.
2. – inversely proportional to the density of the liquid.
3. – directly proportional to the surface tension of the liquid.

Hence, a liquid rises more in a narrower tube ( having less diameter ) than in wider tube ( having larger diameter).

Capillary rise in tube of insufficient height

The height to which a liquid rises in a capillary tube is given by –

h = \left ( \frac {2 \sigma \cos \theta}{\rho g r} \right )

The radius ( r ) of the capillary tube and radius of curvature ( R ) of the liquid meniscus are related by –

r = R \cos \theta

Therefore, \quad h = \left ( \frac {2 \sigma \cos \theta}{\rho g R \cos \theta} \right ) = \left ( \frac {2 \sigma}{R \rho g} \right )

As \sigma, \rho \text {and} g are constants, so \quad h R = \left ( \frac {2 \sigma}{\rho g} \right ) ( It is a constant ).

Therefore, \quad h R = h' R'

Where ( R' ) is the radius of curvature of the new meniscus at a height ( h' ) .

Hence in a capillary tube of insufficient height, the liquid rises to the top and spreads out to a new radius of curvature ( R' ) is given by

R' = \left ( \frac {h R}{h'} \right )

• But the liquid will not overflow from the tube.