What is Centrifugal Force?
Centrifugal force is a fictitious force ( also called a pseudo force ) which is experienced by an object moving in a curved or circular path. It is directed away from the center of circular path or rotation.
- Magnitude and dimension of centrifugal force is equal to the centripetal force.
- It is an inertial force generated in a rotating frame of reference and causes the objects to thrown away from the centre of rotation.
- Direction of centrifugal force is just opposite of direction of the centripetal force.
- Centrifugal force is a fictitious force because it only comes into action when there is a centripetal force.
- This force depends on the mass of the object, the distance of the object from the center of rotation and the speed of rotation.
- The concept of centrifugal force is used in various rotating devices like washing machines, centrifuge rotors, banked roads, centrifugal pumps etc.
Effects of Centrifugal Force
Consider about a car of weight ( mg ) moving on a circular level road of radius ( r ) with constant speed ( v ) . If the speed is high while taking the turn, the tyres of the car tend to leave the road due to action of centrifugal force and the car is thrown away from the centre of the curve.
The forces of friction are ( f_1 ) and ( f_2 ) at the inner and outer tyres respectively. Since the centrifugal force acts outward, hence the friction forces are acting inwards.
If ( R_1 ) and ( R_2 ) are the reactions of the ground at the inner and outer tyres, then –
f_1 = \mu \ R_1 \quad and \quad f_2 = \mu \ R_2
Here, ( \mu ) is the coefficient of friction between the tyres and road.
Also, \quad ( R_1 + R_2 ) = mg and total force of friction \quad ( f_1 + f_2 ) = \mu ( R_1 + R_2 ) = \mu . mg
For the car to stay on the road, the maximum force of friction must be equal to or greater than the centrifugal force.
\mu . mg \ge \frac {mv^2}{r}
Or, \quad \left ( \frac {v^2}{rg} \right ) \le \mu \quad or \quad v^2 \le \mu \ rg
Therefore, maximum speed with which the car can turn safely will be –
v_{max} = \sqrt {\mu \ rg}
If the speed exceeds ( v_{max} ) , contact between road and tyres will break, the car will skid and go off the road.
2.Bending of a cyclist towards centre
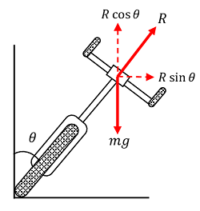
When a cyclist goes round a curved path, the force of friction between the tyres and road is too small to provide the necessary centripetal force. This is the reason that a cyclist going round a curve leans inward so that the reaction of the road is inclined towards centre from vertical and its horizontal component provides the necessary centripetal force.
Suppose the cyclist bends inwards through an angle ( \theta ) from the vertical. The horizontal component of the normal reaction ( R ) provides the necessary centripetal force.
Therefore, \quad R \sin \theta = \left ( \frac {m v^2}{r} \right ) …………….. (1)
The vertical component of normal reaction ( R \cos \theta ) , balances the weight ( mg ) of the cycle and the cyclist.
Therefore, \quad R \cos \theta = mg ………………….. (2)
Dividing equation (1) by equation (2), we will get –
\left ( \frac {R \sin \theta}{R \cos \theta} \right ) = \left ( \frac {m v^2 / r}{mg} \right )
So, \quad \tan \theta = \left ( \frac {v^2}{rg} \right )
Or, \quad \theta = \tan^{-1} \left ( \frac {v^2}{rg} \right )
Thus, the angle ( \theta ) through which the cyclist bends would be greater, if –
- The radius of the curved path is small or the curved turn is sharp.
- The speed of the cyclist is large.
What is Banking & Super Elevation?
The large amount of friction developed between the tyres and the road produces wear and tear of the tyres. To avoid this, the curved road is given an inclination sloping upwards towards the outer circumference. This reduces wearing out of the tyres because the horizontal component of the normal reaction provides the necessary centripetal force.
The system of raising the outer edge of a curved road above its inner edge is called banking of the curved road. The angle through which the outer edge of the curved road is raised above its inner edge is called angle of banking.
Similarly, in movement of vehicles on railway tracks, the centripetal force is provided by the thrust of the rails on the wheel flanges. This causes wearing out of the wheels or rails rapidly. To avoid this, the track is made sloping towards the centre so that the reaction of the track is inclined to the vertical and its horizontal component provides the necessary centripetal force. A track which is made sloping in this manner is called a banked track.
In case of rail tracks, the outer rail is slightly raised above the inner rail. This excess elevation of the outer rail over the inner rail is called super-elevation.
Maximum Speed on Banked track
Consider a car of weight ( mg ) going along a curved path of radius ( r ) with speed ( v ) on a road banked at an angle ( \theta ) .
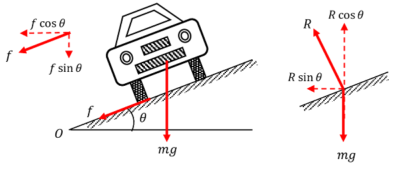
The forces acting on the car are –
- Weight ( mg ) of the car acting vertically downwards.
- Normal reaction ( R ) of the road acting at an angle ( \theta ) with the vertical.
- Force of friction ( f ) acting downwards along the inclined plane.
R \sin \theta + f \cos \theta = \left ( \frac {m v^2}{r} \right ) ……….. (1)
Resolving these forces along horizontal and vertical directions, we will get –
R \sin \theta + f \cos \theta = \left ( \frac {m v^2}{r} \right ) ……….. (1)
And, \quad mg + f \sin \theta = R \cos \theta \quad . Where, \quad f = \mu R
Or, \quad R \cos \theta - f \sin \theta = mg ……… (2)
Dividing equation (1) by equation (2), we will get –
\left [ \frac {R \sin \theta + f \cos \theta}{R \cos \theta - f \sin \theta} \right ] = \left ( \frac {v^2}{rg} \right )
Dividing numerator and denominator of left hand side expression by ( R \cos \theta ) , we will get –
\left [ \frac {\tan \theta + \frac {f}{R}}{1 - \frac {f}{R} \tan \theta} \right ] = \left ( \frac {v^2}{rg} \right )
Or, \quad \left [ \frac {\tan \theta + \mu}{1 - \mu \tan \theta} \right ] = \left ( \frac {v^2}{rg} \right )
Or, \quad v^2 = rg \left [ \frac {\tan \theta + \mu}{1 - \mu \tan \theta} \right ]
Or, \quad v = \sqrt {rg \left [ \frac {\tan \theta + \mu}{1 - \mu \tan \theta} \right ]}
Or, \quad v_{max} = \sqrt {rg \left [ \frac {\tan \theta + \mu}{1 - \mu \tan \theta} \right ]} ……… (3)
For a flat road ( \theta = 0 ) . Therefore, \left [ v_{max} = \sqrt {\mu \ rg} \right ] …….. (4)
Comparing equations (3) and (4), we will get –
\sqrt {rg \left [ \frac {\tan \theta + \mu}{1 - \mu \tan \theta} \right ]} > \left [ \sqrt {\mu \ rg} \right ] Because ( \tan \theta > 0 )
Therefore, by banking of roads, the value of \left ( v_{max} \right ) can be increased.
Difference between Centripetal Force & Centrifugal Force
Centripetal force and Centrifugal force are very confusing. A clear understanding of differences between these two force concepts is required.
| Sl. No. | Centripetal Force | Centrifugal Force |
| 1 | Centripetal force is the force necessary to make a body to move in a circle. | Centrifugal force is the force acting on body as a reaction force of centripetal force. |
| 2 | This force is generated in the form of friction, gravity, tension in a rope etc. | This force is generated only due to existence of centripetal force. |
| 3 | It is a real force. | It is a pseudo ( fictitious ) force. |
| 4 | This force acts along radius and directed towards the center of the circle of motion. | This force acts in radial direction and directed away from the center of the circle of motion. |
