What is a Micro Manometer?
A micro manometer is used for precise measurement of pressure. In micro manometer, the device is made sensitive by making one limb of U tube much larger i.e. about ( 100 ) times more cross section than that of the other limb.
- This manometer is used for precise measuring of low pressures.
- Hence, it is also called a sensitive manometer.
Though there are many types of micro manometers, yet the following two types are most important –
- Vertical tube type.
- Inclined tube type.
Vertical tube Micro Manometer
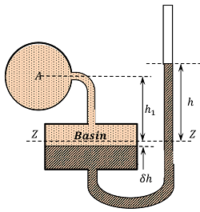
Consider a vertical tube micro manometer connected to a pipe containing light liquid under a very high pressure as shown in figure.
The pressure in the pipe will force the light liquid to push the heavy liquid in the basin downwards. Due to larger area of the basin, the fall of heavy liquid in the basin will be very small. This downward movement of heavy liquid in the basin, will cause a considerable raise of the heavy liquid in the right limb. Let us consider datum line ZZ corresponding to heavy liquid level before the measurement.
Let –
- ( \delta h ) is fall of heavy gauge liquid level in the basin in cm.
- ( h_1 ) is height of light liquid above the datum line in cm.
- ( h ) is height of heavy liquid in the right limb above the datum line in cm.
- ( h_A ) is pressure in the pipe expressed in terms of head of water in cm.
- ( A ) is cross sectional area of the basin in cm^{2} .
- ( a ) is cross sectional area of the tube in cm^2 .
- ( s_1 ) is specific gravity of the light liquid in pipe line.
- ( s ) is specific gravity of the heavy liquid in manometer.
Reading Calculations
We know that, the fall of heavy liquid level in the basin, will cause a corresponding rise of heavy liquid level in vertical tube.
Therefore, \quad ( A \delta h ) = ( a h )
Or, \quad ( \delta h ) = \left ( \frac {a}{A} \right ) \times h ……… (1)
Pressure in the left limb above the datum line is –
( h_A +s_1 h_1 + s_1 \delta h ) Cm of water. ……. (2)
And pressure in the right limb above the datum line is –
( s h + s \delta h ) Cm of water. ……… (3)
Equating these two pressures –
( h_A + s_1 h_1 + s_1 \delta h ) = ( s h + s \delta h )
So, \quad h_A = ( s h + s \delta h - s_1 h_1 - s_1 \delta h )
= \left [ s h - s_1 h_1 + \delta h \left ( s - s_1 \right ) \right ]
Substituting the value of ( \delta h ) from equation (1) –
h_A = \left [ s h - s_1 h_1 + \left ( \frac {a}{A} \right ) h \left ( s - s_1 \right ) \right ] …….. (4)
- Sometimes, the cross sectional area ( A ) of the basin is made very large compared to that of the area ( a ) of tube.
Then, the ratio \left ( \frac {a}{A} \right ) becomes extremely small and thus it can be neglected.
Therefore, the above equation becomes [ h = ( s h - s_1 h_1 ) ] …….. (5)
Inclined tube Micro Manometer
To make a manometer more sensitive and for giving more precise reading, the vertical tube of micro manometer is made inclined and then it is called an inclined tube micro manometer.
An inclined tube micro manometer is shown in figure. Due to inclination of the tube, the distance moved by heavy liquid in the narrow tube is more and thus gives higher readings for very low pressure. Thus, the device become more sensitive.
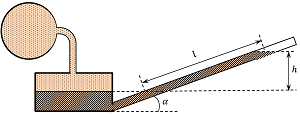
From geometry of figure, we find that –
\left ( \frac {h}{l} \right ) \sin \alpha
So, \quad h = l \sin \alpha
By substituting the value of ( h ) in the micro manometer equation (5), we can find out the required pressure in the pipe.
