What is Earth’s Magnetic Field?
Our earth behaves as a magnet and its magnetic field is called earth’s magnetic field.
Magnetic field of the earth changes from place to place and time to time on the surface. This change in earth’s magnetic field is due to solar winds. Solar wind consists of electron and proton like charged particles. These particles are trapped in the earths magnetic poles and affect the variation of earth’s magnetic field.
Geo-magnetism
The study of Earth’s magnetism is known as Geo-magnetism or Terrestrial magnetism or Earth’s magnetism.
Cause of Earth’s Magnetism
Many possible causes have explained for geo-magnetism. These are as follows –
- Earth’s atmosphere consists of electric charged particles i.e. electrons and ions. These charged particles are in motion due to the rotation of earth. The motion of these charged particles set up electric currents which may be the cause of earth’s magnetism.
- Earth has charged molten fluid. The charged fluid rotates along with earth and sets up currents which may be the cause of earth’s magnetism. This is known as Dynamo effect.
- Every substance on the earth consists of charged particles like protons and electrons. When earth rotates, these charged particles set up circulating currents which may be the cause of earth’s magnetism.
- It is considered that the cause of earth’s magnetic field is due to the circulating electric currents set up inside the earth mass which produces magnetic field.
Features of Earth’s Magnetic Field
The magnetic field lines of earth’s magnetic field are shown in figure. It has the following features –
Earth’s Magnetic Poles
Earth’s magnetism may be assumed to be due to a huge bar magnet buried inside the earth. The axis of this bar magnet is inclined at an angle of 11.3 \degree W of the axis of rotation of the earth. The axis of rotation of the earth is called geographical axis and the axis of bar magnet is called magnetic axis. In the figure ( S_M-N_M ) is the magnetic axis of earth.
The South pole ( S_M ) of this magnet is towards the geographical North ( N_G ) and its North pole ( N_M ) is towards the geographic South ( S_G ) as shown in figure above.
Earth’s Magnetic Field lines
The magnetic field lines due to earth’s magnetism are parallel to the earth’s surface near the magnetic equator and are perpendicular to the earth’s surface near the magnetic poles.
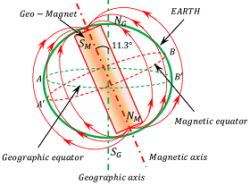
Earth’s magnetic field lines are shown in figure.
Geographical axis of Earth
An imaginary line joining the geographic poles i.e. north pole ( N_G ) and geographic south pole ( S_G ) of the earth is called geographical axis.
Geographical axis is the axis of rotation of earth.
Magnetic axis of Earth
The line joining the magnetic poles i.e. magnetic north pole ( N_M ) and magnetic south pole ( S_M ) of earth’s magnet is called magnetic axis. It makes an angle of about ( 11.3 \degree ) towards west with the geographical axis.
Geographic Meridian
A vertical plane which passes through the geographical axis is called geographic meridian.
In figure ( B ), green colored plane represents Geographic meridian.
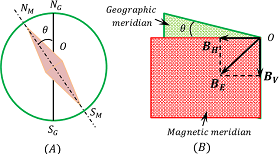
Magnetic Meridian
A vertical plane which passes through the magnetic axis is called magnetic meridian.
In figure ( B ), red colour plane represents Magnetic meridian of earth. It makes an angle of ( \theta = 11.3 \degree ) with the Geographic meridian as shown in figure ( B ).
Elements of Earth’s Magnetic Field
The magnitude and direction of earth’s magnetic field at a place on the earth’s surface is completely defined by specifying three different quantities –
- Magnetic declination.
- Magnetic inclination or dip.
- Horizontal component of magnetic field.
These elements are called elements of geo-magnetism or elements of Earth’s magnetic field.
Magnetic Declination (D)
Magnetic declination ( \theta ) at a place on the earth’s surface is defined as the angle between geographic meridian and magnetic meridian at that place.
If a magnetic needle is suspended freely at a place on the earth’s surface, it will lie in a direction parallel to the magnetic meridian at that place. The North pole of the needle will point towards the magnetic North pole and vice versa.
Figure (A) shows the stable position of a freely suspended magnetic needle at a place. The angle ( \angle N_M O N_G ) is magnetic declination ( \theta ) . Declination is also represented by symbol ( D ) .
In other words –
The angle ( \theta ) between the North directed by a freely suspended horizontal compass needle and the true geographic North is called declination.
- Declination ( \theta ) is less near the equator and more at higher latitudes.
- Declination in India is small. It is about ( 0 \degree 50' \ W ) in Mumbai.
Magnetic Inclination (DIP)
Magnetic Inclination or Dip at a place on earth’s surface is the angle between the direction of total intensity of magnetic field of earth at that place and a horizontal line in the magnetic meridian.
In figure (B), ( OB_E ) represents total intensity of magnetic field. ( OB_E ) makes an angle ( \delta ) with a horizontal line ( OB_H ) in the magnetic meridian.
The angle ( \delta ) is called as Dip at that place. It is also represented by ( I ) (means inclination).
- The North pole tip of freely suspended magnetic needle dips by an angle ( \delta ) from horizontal line.
- Value of ( \delta ) is ( 0 \degree ) at equator and ( 90 \degree ) at poles.
- Dip is about ( 42 \degree ) at Delhi.
Horizontal component of Magnetic Field (B)
The horizontal component of total magnetic field of earth at a point in magnetic meridian is called horizontal component of earth’s magnetic field.
In figure above, ( B_H ) is the horizontal component and ( B_V ) is the vertical component of intensity of earth’s magnetic field.
Then, \quad B_H = B_E \cos \delta ….. (1)
And \quad B_V = B_E \sin \delta ….. (2)
Therefore, \quad \left ( \frac {B_V}{B_H} \right ) = \left ( \frac {B_E \sin \delta}{B_E \cos \delta} \right ) = \tan \delta
Or, \quad \tan \delta = \left ( \frac {B_V}{B_H} \right ) …….. (3)
Also by squaring and adding equations (1) and (2) we get –
( B_H^2 + B_V^2 ) = ( B_E^2 \cos^2 \delta + B_E^2 \sin^2 \delta )
= B_E^2 ( \cos^2 \delta + \sin^2 \delta ) = B_E^2
Therefore, \quad B_E = \sqrt {B_H^2 + B_V^2} ………. (4)
See numerical problems based on this article.
