Kinetic Theory of Gases

What is the Kinetic Theory of Gases?

Kinetic theory of gases is used as a framework for understanding gases and predicting their behavior. It links the microscopic behavior of gas molecules to the macroscopic properties of gases.

Kinetic theory of gases is based on following assumptions about gas molecules –

1. Gases consist of many molecules which are in constant and random motion in straight lines.
2. Molecules are rigid, elastic spheres and identical in all respect for a given gas and different for different gases.
3. The size of all the molecules is negligible as compared with the total volume of gas.
4. Inter molecular forces between gas molecules are negligible.
5. The average kinetic energy of all molecules does not change so long as the gas temperature is constant.
6. During the random motion molecules collide with one another and also with walls of container.
7. These collisions are instantaneous and perfectly elastic.
8. The average kinetic energy of all molecules is proportional to the absolute temperature of the gas.

These assumptions results that at any temperature gas molecules in equilibrium will have the same average kinetic energy (but not necessary that the molecules will have same velocity and mass).

Expression for Pressure from Kinetic Theory of Gases

Consider that an ideal gas having mass ( M ) is enclosed in a cubical vessel as shown in figure. Let –

• Length of each side of cube is ( l ) .
• Therefore volume of cube will be \left ( V = l^3 \right ) .
• Let, ( n ) is the number of molecules per unit volume of gas.
• ( m ) is the mass of each molecule.

Consider that a molecule moving with velocity ( v ) hits a wall perpendicular to X axis of container. Before collision, the components of molecule velocity are –

( v_x, \ v_y, \ v_z )

Because the collisions are elastic, the molecule will rebound with the same velocity. The y-component and z-component of velocity will not change but the x-component of velocity will reverse its sign.

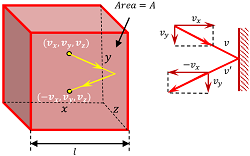
Therefore, velocity of the molecule after collision will be –

( - v_x, \ v_y, \ v_z )

Therefore, change in momentum of the molecule will be –

\Delta p = m v_x - ( - m v_x ) = 2 m v_x

Hence, by the law of conservation of momentum, the momentum imparted to the wall in each collision will be –

\Delta p = 2 m v_x

• The distance moved by a molecule between two successive collisions with this face is 2l .
• Then time interval between two collisions with this face will be \left ( \frac {2l}{v_x} \right ) .
• Therefore, number of collisions per unit time with this face will be \left ( \frac {v_x}{2l} \right )

Hence, change in momentum per unit time at this face –

\left ( \frac {\Delta p}{t} \right ) = 2m v_x \left ( \frac {v_x}{2l} \right )

= \left ( \frac {m v^2_x}{l} \right )

By Newton’s laws of motion, change in momentum per unit time is the force.

Therefore, force exerted on this face will be –

\text {Force} = \text {Change in momentum per unit time}

Therefore, \quad F_x = \frac {\Delta p}{t} = \left ( \frac {m {v_x}^2}{l} \right )

Let, ( n ) is the number of molecules per unit volume. Therefore, total number of molecules in cube will be –

N = \left ( n l^3 \right )

Let, \quad \left ( \bar {v_x}^2 \right ) is the average of the squares of the X-component velocities of all molecules.

Then, average force on this face will be –

\text {Average force} = \text {Number of molecules} \ \times \ \text {Momentum imparted by one molecule}

Or, \quad F_{total} = N \left ( \frac {m \bar {v_x}^2}{l} \right )

= N \left ( \frac {m}{l} \right ) \ \bar {v_x}^2

Assuming the gas is isotropic, so the molecular velocities are equally distributed in all directions.

Therefore, by symmetry –

\bar {v_x}^2 = \bar {v_y}^2 = \bar {v_z}^2

= \left ( \frac {1}{3} \right ) \bar {v}^2

Where, ( \bar {v}^2 ) is the root mean square velocity of molecules.

Therefore, average pressure on this wall will be –

P = \frac {\text {Total force}}{\text {Area}}

= \left [ \frac {N \left ( \frac {m}{l} \right ) \ \bar {v_x}^2}{l^2} \right ] = N \left ( \frac {m}{l^3} \right ) \ \bar {v_x}^2

= N \left ( \frac {m}{V} \right ) \left ( \frac {1}{3} \right ) \bar {v}^2 = \left ( \frac {1}{3} \right ) m \left ( \frac {N}{V} \right ) \bar {v}^2

= \left ( \frac {1}{3} \right ) \ m \ n \ \bar {v}^2 ……… (1)

Also, \quad P = N \left ( \frac {m}{V} \right ) \left ( \frac {1}{3} \right ) \bar {v}^2

= \left ( \frac {Nm}{V} \right ) \left ( \frac {1}{3} \right ) \bar {v}^2

= \left ( \frac {M}{V} \right ) \left ( \frac {1}{3} \right ) \bar {v}^2

= \left ( \frac {1}{3} \right ) \rho \bar {v}^2 ………. (2)

Because, \quad Nm = M (Total mass of gas).

Also \quad \left ( \frac {M}{V} \right ) = \rho (Density of gas).

Kinetic Energy from Kinetic Theory of Gases

According to kinetic theory of gases, the pressure exerted by a gas of density ( \rho ) and RMS velocity ( v )  is given by –

P = \left ( \frac {1}{3} \right ) \rho \ v^2

Average kinetic energy of translation per unit volume of gas will be –

E' = \left ( \frac {1}{2} \right ) \times \text {( Mass / Volume )} \times \text {( velocity )}^2 = \left ( \frac {1}{2} \right ) \rho \ v^2

Therefore, \quad \left ( \frac {P}{E'} \right ) = \left [ \frac {\left ( \frac {1}{3} \right ) \rho v^2 }{\left ( \frac {1}{2} \right ) \rho v^2 } \right ]

= \left ( \frac {2}{3} \right )

So, \quad P = \left ( \frac {2}{3} \right ) E'

Therefore, \quad \text {Pressure} = \left ( \frac {2}{3} \right ) \times \text {Average KE per unit volume} .

Hence, pressure exerted by a gas is equal to two-thirds of average kinetic energy of translation per unit volume of gas.

Kinetic Interpretation of Temperature

Consider that, ( M ) is the molecular mass of gas and root mean square ( RMS ) velocity of molecules is ( v ) .

Then, average kinetic energy of translation per mole of gas will be –

E = \left ( \frac {1}{2} \right ) M v^2

From kinetic theory of gases, the pressure exerted by a gas of density ( \rho ) is –

P = \left ( \frac {1}{3} \right ) \rho \ v^2

= \left ( \frac {1}{3} \right ) \left ( \frac {M}{V} \right ) v^2

So, \quad P V = \left ( \frac {1}{3} \right ) M \ v^2

= \left ( \frac {2}{3} \right ) \times \left ( \frac {1}{2} \ M \ v^2 \right )

= \left ( \frac {2}{3} \right ) E

Also for one mole of a gas we know –

P V = R T

So, \quad \left ( \frac {2}{3} \right ) E = R T

Or, \quad E = \left ( \frac {3}{2} \right ) RT

If, ( N ) is the Avogadro’s number,

Then kinetic energy per molecule  \quad \bar {E} = \left ( \frac {E}{N} \right )

= \left [ \frac { \left ( \frac {3}{2} \right ) RT }{ N } \right ]

= \left ( \frac {3}{2} \right ) \left ( \frac {R}{N} \right ) T

= \left ( \frac {3}{2} \right ) k_B \ T , where ( k_B ) is the Boltzmann’s constant.

Therefore, \quad \bar {E} \propto T

Also, \quad \bar {E} = \left ( \frac {3}{2} \right ) k_B \ T

Hence, mean kinetic energy per molecule of a gas is proportional to the absolute temperature of the gas. It is independent of the pressure, volume and nature of the ideal gas.