What is meant by Centre of Gravity?
Centre of gravity of a body is a fixed point where total weight of body is assumed to be concentrated. It is the point through which, force of gravity acts on the body.
We know that, a body is constructed of many tiny particles. Each tiny particle has its own mass. These tiny masses together constitute the whole mass of that body.
- All these tiny masses are attracted by earth towards its centre with gravitational force proportional to their masses which are called tiny weight particles.
- The system of tiny weight particles of a body can be considered as a system of parallel forces.
- Centre of these parallel forces is the centre of gravity of that body.
- The centre of parallel forces or system of tiny mass particles of body can be determined by Varignon’s theorem.
So, \quad \text {Weight} \ ( w ) \propto \text {Mass} \ ( m )
Or, \quad ( w = mg ) Here ( g ) is called earth’s acceleration due to gravity.
Hence, \quad ( w_1 = m_1 g ), \ ( w_2 = m_2 g ), \ ....... \ ( w_n = m_n g ) etc.
Therefore, \quad W = \sum {w} = \sum {mg} = g \sum {m} = M g
Difference between Centre of Mass and Centre of Gravity
Consider that, a body is made up of ( n ) number of tiny mass particles. Let, masses of these particles are ( m_1 ), \ ( m_2 ), \ ....... ( m_n ) etc.
Centre of mass of a body is a point at which distribution of tiny mass particles in all directions is equal. It is not affected by the value of acceleration due to gravity ( g ) .
Now, weight of tiny mass particles will be –
( w_1 = m_1 g ), \ ( w_2 = m_2 g ), \ ....... \ ( w_n = m_n g ) etc.
These tiny weights are equivalent of forces. Centre of these forces is the centre of gravity of that body.
Therefore, earth’s acceleration due to gravity ( g ) is the only distinguishing factor between centre of mass and centre if gravity. The basic differences between these two are as follows –
| Parameter | Centre of Mass | Centre of Gravity |
| Location of point. | It is the point at which total mass of a body is assumed to be concentrated. | It is the point at which total weight of the body is assumed to be concentrated. |
| Distribution of mass. | It is the point about which distribution of tiny mass particles in all direction is equal. | It is the point about which distribution of tiny weight particles in all direction is equal. |
| Factor affecting difference. | Earth’s acceleration due to gravity ( g ) has no effect on centre of mass. | Earth’s acceleration due to gravity ( g ) affects the position of centre of gravity. |
| Variation in position of point. | It’s position is fixed for a certain body. | If an object is so large that value of ( g ) is different at different locations on body part, then centre of mass and centre of gravity will be at different points. |
TO BE NOTED –
- The terms centre of gravity and centre of mass are interchangeably used.
- On the earth’s surface the value of ( g ) is same for all tiny mass particles of a body.
- Therefore, center of gravity is exactly at same position as that of center of mass.
- But for a very large body, if the value of ( g ) is considerably different at different locations on body part then, centre of gravity and centre of mass will not be at the same point.
See the numerical problems based on this article –
Steps to find Centre of Gravity
There are two simple steps to find the centre of gravity. (1) Determination of centre of gravity by symmetry and (2) Determination of centre of gravity by integration.
1.Centre of Gravity by Symmetry
We have discussed about finding the centre of mass by symmetry of a body. In the same way we can use the principle of symmetry to find the ( COG ) of a body.
Here, we will discuss only about the integration method in detail to find the centre of gravity of a body.
2.Centre of Gravity by Integration
Integration method is conveniently used to find the centre of gravity of irregular shaped objects. This involves the following steps –
STEP 1 – DRAW A SKETCH OF BODY WITHIN CO-ORDINATE AXES
Consider about a solid body of irregular shape as shown in figure.
Draw a free hand sketch of the object within the reference axes XX' axis and YY' axis. A rough sketch without any projection or scaling is sufficient for this purpose. Now, position of centre of gravity of the body is find out with respect to the axes.
STEP 2 – CUT ELEMENTARY STRIPS
Imagine two cutting planes very close to each other. These cutting planes are parallel to the YY' axis and passing through at distances of ( x ) and ( x + dx ) and cut an elementary strip ABCD .
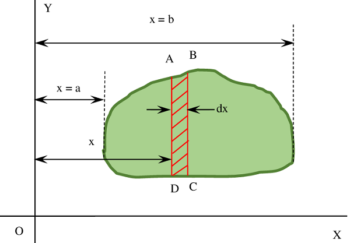
Width of this elementary strip will be ( dx ) . Let, its length is ( L ) . Then area of elementary strip is \quad ( da ) = ( L \times dx )
Since, width ( dx ) is very small, so the shaded area ABCD can be considered as a rectangle.
Here, the length of strip ( L ) is a variable which depends on the distances of cutting planes. So, length ( L ) can be represented in terms of another variable ( x ) .
Now, using geometric and trigonometric relations, the length ( L ) is expressed in terms of variable ( x ) , so that integration can be performed conveniently.
STEP 3 – FIND CENTRE OF GRAVITY OF STRIP
Since, elementary strip ABCD is a rectangle, so its centre of gravity will be at a distance of \left [ x + \left ( \frac {dx}{2} \right ) \right ] from YY' axis.
But, ( dx ) is very small. Hence \left ( \frac {dx}{2} \right ) can be neglected.
Therefore, \quad \left [ x + \left ( \frac {dx}{2} \right ) \right ] = x
Hence, centre of gravity of elementary strip of area ( da ) is at a distance of ( x ) units from YY' axis.
Moment of this area about YY' axis will be –
dM = da \times x = x da
STEP 4 – DIVIDE WHOLE OBJECT IN NUMEROUS STRIPS
Using similar cutting planes, the whole object is assumed to cut into several elementary strips. Distances ( x ) for these cutting planes will be different for different strips which will lie between the dimensions of extreme ends of body i.e. from \left ( x = a \right ) to \left ( x = b \right ) .
Therefore, limits of integration will be from \left ( x = a \right ) to \left ( x = b \right ) .
STEP 5 – APPLY INTEGRATION METHOD
By definition, the distance of point ( COG ) of body will be ( \bar {X} ) –
\bar {X} = \left [ \frac {\left ( dm_1 x_1 \right ) + \left ( dm_2 x_2 \right ) + ....... + \left ( dm_n x_n \right )}{\left ( dm_1 + dm_2 + ..... + dm_n \right )} \right ]
Here, \left ( dm_1 x_1 \right ), \ \left ( dm_2 x_2 \right ), \ ....... \left ( dm_n x_n \right ) etc. are moments of elementary masses about YY' axis.
Let, ( \sigma ) is the mass per unit area of the material of object.
Therefore, \quad dm = \sigma da
Hence, ( dm_1 = \sigma da_1 ), \ ( dm_2 = \sigma da_2 ), ............ \ ( dm_n = \sigma da_n ) etc.
Therefore, \quad \bar {X} = \left [ \frac {\sigma \left ( da_1 x_1 + da_2 x_2 + ....... + da_n x_n \right )}{\sigma \left (da_1 + da_2 + ..... + da_n \right )} \right ]
= \left [ \frac { \left ( da_1 x_1 + da_2 x_2 + ....... + da_n x_n \right )}{ \left (da_1 + da_2 + ..... + da_n \right )} \right ]
= \sum_{x=b}^{x=a} x da = \sum_{x=b}^{x=a} x Ldx
Here, it is essential to express ( L ) in terms of variable ( x ) . In doing this let, length \quad L = p \ x^{q} where ( p \ \text {and} \ q ) are constants.
Therefore, \quad \bar {X} = \int\limits_{b}^{a} x L dx
= \int\limits_{b}^{a} ( x ) \ ( p \ x^{q} ) dx
= p \int\limits_{b}^{a} x^{( q+1 )} dx
Integrating this expression, we can find the distance of ( COG ) of object from YY' axis.
In similar way, repeating the steps 1 to 5, we can get distance of ( COG ) of object from XX' axis.
Therefore, \quad \bar {Y} = \int\limits_{c}^{d} y L dy
Here ( c ) and ( d ) are the extreme bottom and upper points of body i.e. limits of integration will be from \left ( y = c \right ) to \left ( y = d \right ) .
In this way, centre of gravity of any solid body can be determined by integration method.
Centre of Gravity of solids
Centre of gravity of some common solid bodies, obtained by integration method are as follows –
| Sl No. | Shape of solid. | Datum line or plane. | Distance of centre of gravity |
| 1 | Semi circular arc. | Diameter. | \left ( \frac {2r}{\pi} \right ) |
| 2 | Right circular cone. | Base plane. | \left ( \frac {h}{4} \right ) |
| 3 | Right circular hollow cone. | Base plane. | \left ( \frac {h}{3} \right ) |
| 4 | Solid hemisphere. | Base plane. | \left ( \frac {3r}{8} \right ) |
| 5 | Hollow hemisphere. | Base plane. | \left ( \frac {r}{2} \right ) |
Here, ( h ) is height and ( r ) is radius.
See numerical problems based on this article.
