How energy change occurs in Simple Harmonic Motion?
The total energy in Simple Harmonic Motion is consisting of two parts –
Kinetic energy in Simple Harmonic Motion
Velocity of a particle in simple harmonic motion is given by –
v = - \omega A \sin ( \omega t + \phi _ { 0 } )
Hence, kinetic energy of the particle at any position will be –
K = \left ( \frac { 1 }{ 2 } \right ) m v ^ 2
= \left ( \frac {1}{2} \right ) m [ - \omega A \sin ( \omega t + \phi _ { 0 } ) ]^2
= \left ( \frac { 1 }{ 2 } \right ) m \omega ^ 2 A ^ 2 \sin ^ 2 ( \omega t + \phi _ { 0 } )
But, \quad A ^ 2 \sin ^ 2 ( \omega t + \phi _ { 0 } ) = ( A ^ 2 - x ^ 2 )
Therefore, from equation (1), we will get –
K = \left ( \frac {1}{2} \right ) m \omega^2 ( A ^ 2 - x ^ 2 )
For restoring force or force constant in simple harmonic motion –
\omega ^2 = \left ( \frac { k }{ m } \right )
Or, \quad K = \left ( \frac {1}{2} \right ) k ( A ^ 2 - x ^ 2 )
Therefore, kinetic energy of particle in simple harmonic motion has following characteristics –
- Variation of kinetic energy is periodic in nature. But it is not a simple harmonic activity.
- Kinetic energy varies from minimum value ( at extreme positions ) to maximum value ( at mean position ) and vice versa. It happens twice in one complete cycle.
- Therefore, kinetic energy completes 2 cycles in duration of 1 cycle of simple harmonic motion.
Potential energy in Simple Harmonic Motion
For a particle in simple harmonic motion, the restoring force is given by –
F = - k x
Let, the particle is further displaced through a small distance ( dx ) . Then work done against the restoring force will be –
d W = - F d x = (+ k x ) d x
Therefore, total work done in moving the particle from mean position to a point of displacement ( x ) is given by –
W = \int d W = \int\limits _ { 0 }^{ x } (+ k x) d x
Or, \quad W = k \left [ \frac { x ^ 2 }{ 2 } \right ] _ { 0 }^{ x } = \left ( \frac { 1 }{ 2 } \right ) k x ^ 2
This work is stored as potential energy in the particle.
Therefore, \quad U = \left ( \frac { 1 }{ 2 } \right ) k x ^ 2
= \left ( \frac { 1 }{ 2 } \right ) m \omega ^ 2 x ^ 2
= \frac { 1 }{ 2 } m \omega ^ 2 A ^ 2 \cos ^ 2 ( \omega t + \phi _ { 0 } )
Therefore, for a particle in simple harmonic motion, potential energy has following characteristics –
- Variation of potential energy is periodic in nature but it is not a simple harmonic activity.
- Potential energy varies from minimum value ( at mean position ) to maximum value ( at extreme positions ) and vice versa. It happens twice in one cycle of simple harmonic motion.
- Therefore, potential energy completes 2 cycles in duration of 1 cycle of simple harmonic motion.
Total energy in Simple Harmonic Motion
At any position of displacement, the total energy of simple harmonic motion is given by –
E = ( K + U )
= \left [ \left ( \frac { 1 }{ 2 } \right ) k ( A ^ 2 - x ^ 2 ) + \left ( \frac { 1 }{ 2 } \right ) k x ^ 2 \right ]
= \left ( \frac {1}{2} \right ) k A^2
= \left ( \frac { 1 }{ 2 } \right ) m \omega ^ 2 A ^ 2
= \left ( \frac {1}{2} \right ) m \left ( \frac {2 \pi}{T} \right )^2 A^2
= 2 \pi ^ 2 m \nu ^ 2 A ^ 2
Because, \quad \left [ \left ( \frac {1}{T} \right ) = \nu \right ]
Therefore, in simple harmonic motion –
- Total mechanical energy is directly proportional to the mass ( m ) of the particle.
- It is proportional to the square of frequency ( \nu ) .
- Total mechanical energy is directly proportional to the square of amplitude.
- It is independent of time ( t ) and displacement ( x ) .
Variation in total energy along a cycle
Following table shows the variation of kinetic energy ( K ) and potential energy ( U ) at different displacement positions ( x ) .
| Displacement ( x ) | ( x = - A ) | ( x = 0 ) | ( x = + A ) |
| Kinetic energy ( K ) | 0 | \left ( \frac { 1 }{ 2 } \right ) k A ^ 2 | 0 |
| Potential energy ( U ) | \left ( \frac { 1 }{ 2 } \right ) k A ^ 2 | 0 | \left ( \frac { 1 }{ 2 } \right ) k A ^ 2 |
| Total energy ( E ) | \left ( \frac { 1 }{ 2 } \right ) k A ^ 2 | \left ( \frac { 1 }{ 2 } \right ) k A ^ 2 | \left ( \frac { 1 }{ 2 } \right ) k A ^ 2 |
The variations of ( K ) and ( U ) with respect to displacement ( x ) is plotted as shown in figure.
From figure, it is evident that –
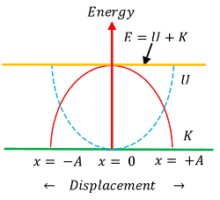
- Graph for kinetic energy ( K ) and potential energy ( U ) with respect to the displacement position ( x ) is parabolic curve. But total energy curve is a straight line parallel to the displacement axis.
- Both kinetic energy ( K ) and potential energy ( U ) are periodic functions of time. The period of each being \left ( \frac {T}{2} \right )
- At ( x = 0 ) , the potential energy is zero and total energy is the kinetic energy.
- At ( x = \pm A ) , the kinetic energy is zero and total energy is the potential energy.
- In each cycle of simple harmonic motion, both kinetic energy and potential energy acquire their peak values twice.
See numerical problems based on this article.
