“Laws of Forces” Numerical Problems
Try to solve the following “Laws of Forces” numerical problems to clear the concepts in solving the numerical problems.
First of all go to the theory portion of the respective topic and then try to solve the numerical problems by yourself. If facing problem in solving the numerical, click on the Go to solution button to see the ready made solution placed at the bottom of each numerical problem.
01) PROBLEM – P020101
The resultant of two forces is ( 8 \ kgwt ) and its direction is inclined at 60 \degree to one of the forces whose magnitude is ( 4 \ kgwt ) .
Find magnitude and direction of the other force.
Keyword related to this problem.
02) PROBLEM – P020102
Find a point within a quadrilateral as shown in figure such that if it is acted upon by forces represented by lines joining the point to the angular points of the quadrilateral, it will be in equilibrium.
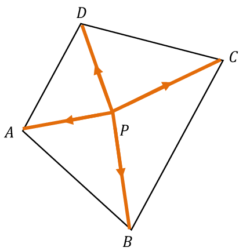
Keywords related to this problem.
03) PROBLEM – P020103
A string ACB of length ( 47.3 \ cm ) is tied to two points A and B at the same level as shown in figure. A smooth ring of weight ( 40 \ kg ) which can freely slide along the string is at C at ( 30 \ cm ) away from A along the string and is pulled by a horizontal force ( P ) .
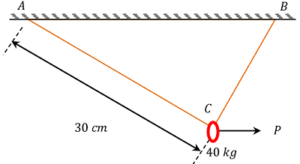
If point C is ( 15 \ cm ) below the level of AB, determine the magnitude of force ( P ) .
Keywords related to this problem.
04) PROBLEM – P020104
Two identical prismatic bars PQ and RS each weighing ( 15 \ kg ) are welded to form a Tee ( T ) and are suspended in a vertical plane as shown in figure.
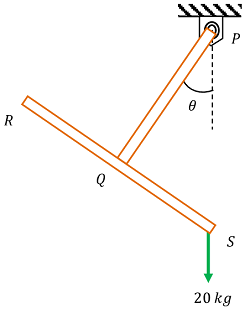
Calculate the value of angle ( \theta ) that the bar PQ will make with vertical when a vertical load of ( 20 \ kg ) is applied at point S.
Keyword related to this problem.
05) PROBLEM – P020105
Figure below shows a body under the action of co-planar forces.
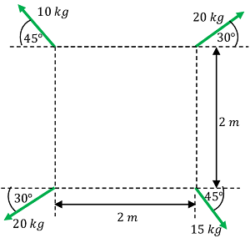
Determine the magnitude, direction and position of a single force which will keep the body in equilibrium.
Keywords related to this problem.
- Parallelogram law of addition of forces.
- Moment of a force.
- Couple of a force.
- Conditions of static equilibrium.
06) PROBLEM – P020106
Find the value of the angle ( \theta ) in figure if block B is about to slide.
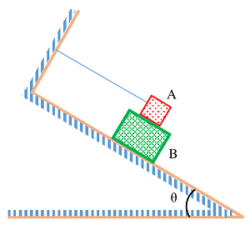
Weight of block A is ( 10 \ kg ) and that of the block B is ( 20 \ kg ) and ( \mu = 0.25 ) for all surfaces.
Keywords related to this problem.
- Resolution of a force into rectangular components.
- Free body diagram.
- Conditions of static equilibrium.
- Coefficient of friction.
07) PROBLEM – P020107
A block of weight ( W_1 = 100 \ kgf ) rests on a horizontal surface and supports on top of it another block of weight ( W_2 = 25 \ kgf ) as shown in figure.
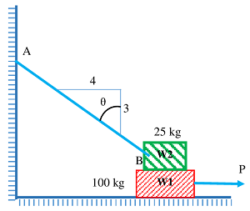
The block W_2 is attached to a vertical wall by an inclined string AB . Find the magnitude of the horizontal force ( P ) applied to the lower block as shown that will be necessary to cause slipping to impend. The coefficient of static friction for all surfaces is ( \mu = 0.3 )
Keywords related to this problem.
08) PROBLEM – P020108
A uniform rod of length ( 10 \ cm ) is placed with one end inside a smooth hemispherical bowl. Axis of bowl is vertical and radius is ( 4 \ cm ) .
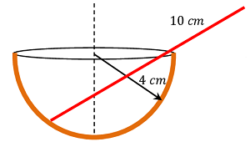
Find the inclination of the rod to the horizontal and the length which projects out of the bowl.
Keywords related to this problem.
09) PROBLEM – P020109
A uniform wheel of ( 1000 \ kg ) weight and ( 60 \ cm ) in diameter rests against a rigid rectangular block of ( 15 \ cm ) height as shown in figure.
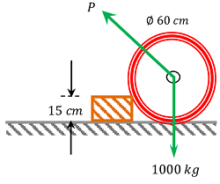
Find the least pull through the centre of the wheel to just turn the wheel over the corner of the block. All surfaces are smooth. Also find the reaction of the block.
Keywords related to this problem.
10) PROBLEM – P020110
Find the maximum tension in the cord shown in figure, if the bodies have developed full friction.
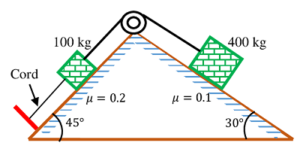
Keywords related to this problem.
- Coefficient of friction.
- Tension in a rope.
- Conditions of static equilibrium.
- Resolution of a force into rectangular components.
11) PROBLEM – P020111
Two blocks which are connected by a horizontal link are supported on two rough planes as shown in figure.
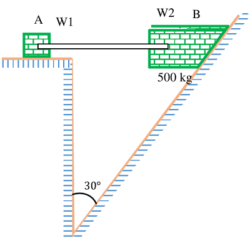
The coefficient of friction for block A is ( 0.4 ) . The angle of friction for the block B on the inclined plane is ( \phi = 20 \degree ) . Find the smallest weight ( W_1 ) of the block A for which equilibrium can exist.
Keywords related to this problem.
