What is Angular Momentum?
Momentum of a moving body is defined as the product of the mass and velocity of the body. It gives an idea about the energy capacity that a moving body possesses.
For a moving body in a curved path –
Angular momentum is defined as a quantity possessed by the body due to inertia of motion. Its magnitude is equal to the product of mass of body and angular velocity.
\text {Angular Momentum} = \text {Mass} \ \times \ \text {Angular Velocity}
Therefore, \quad \vec L = m \vec {\omega}
Angular momentum is also expressed in a different and most convenient way as follows.
Angular momentum of a particle rotating about a fixed axis is defined as the moment of linear momentum of that particle about the axis of rotation.
\text {Angular Momentum} = \text {Linear Momentum} \ \times \ \text {Perpendicular distance from axis of rotation}
Therefore, \quad \vec L = \vec p \ d
Here, ( \vec p ) is linear momentum and ( d ) is the perpendicular distance of linear momentum vector from axis of rotation of particle.
Magnitude of Angular Momentum
Consider about the figure as shown below.
A particle of mass ( m ) is rotating about origin point O and at any instant, the position vector is ( \vec r ) .
Suppose that, the linear momentum vector ( \vec p ) of the particle makes an angle ( \theta ) with the position vector ( \vec r ) as shown in figure.
PN is the line of action of linear momentum vector ( \vec p )
From origin O , a perpendicular ON is drawn.
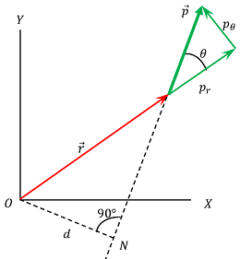
Then from right angled triangle ( \triangle ONP ) , we have –
\left ( \frac {ON}{OP} \right ) = \sin \theta
Or, \quad \left ( \frac {d}{r} \right ) = \sin \theta
Therefore, \quad d = r \sin \theta \quad ( This is the perpendicular distance of line of action of linear momentum from the axis of rotation. )
Therefore, arm of moment or lever arm is ( r \sin \theta )
Hence, angular momentum about point O will be –
L = p \ \times \ r \sin \theta = p ( r \sin \theta ) = p d
So, we can say that angular momentum is the moment of linear momentum. Hence, it is also called as moment of momentum.
Now, the linear momentum vector ( \vec p ) can be resolved into rectangular components –
(i) Radial component \left (p_r \right ) – Its magnitude is ( p \cos \theta ) . It acts along the direction of position vector ( \vec r ) . It doesn’t contribute to the angular momentum.
(ii) Angular or tangential component \left ( p_{\theta} \right ) – Its magnitude is ( p \sin \theta ) . It acts perpendicular to the position vector ( \vec r ) . This component only contribute for angular momentum.
Therefore, magnitude of angular momentum is equal to the product of tangential component of linear momentum and its distance from axis of rotation.
Right Hand Thumb Rule
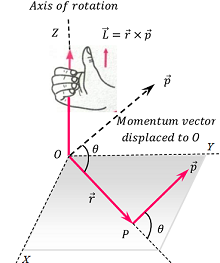
Angular momentum is a vector quantity.
Direction of angular momentum is always perpendicular to the plane containing the position vector ( \vec r ) and linear momentum vector ( \vec p ) . Its sense is determined by the right hand thumb rule as shown in figure.
Right Hand Thumb Rule for direction of angular momentum or torque states that –
If we curl the fingers of our right hand in the direction in which position vector ( \vec r ) is rotated to move into the position of linear momentum vector ( \vec p ) through the smaller angle between them, then the extended thumb gives the sense of angular momentum.
Angular Momentum & Torque
Magnitude of torque acting on a body is given by –
\vec \tau = ( \vec r \times \vec F ) ……… (1)
And, magnitude of angular momentum is given by –
\vec L = ( \vec r \times \vec p ) ………. (2)
Differentiating both sides of equation (2) with respect to ( t ) , we get –
\left ( \frac {d \vec L}{dt} \right ) = \vec p \left ( \frac {d \vec r}{dt} \right ) + \vec r \left ( \frac {d \vec p}{dt} \right )
But, \left ( \frac {d \vec r}{dt} \right ) = v ( Rate of change in position. )
And, \left ( \frac {d \vec p}{dt} \right ) = \vec F ( Rate of change in momentum. )
Hence, \quad \left ( \frac {d \vec L}{dt} \right ) = \left ( \vec p \times \vec v \right ) + \left ( \vec r \times \vec F \right ) ……… (3)
Also, product \quad \left ( \vec p \times \vec v \right ) = ( m \vec v ) \times \vec v = 0 ( Since they have same line of action. )
Therefore, equation (3) reduces to –
\left ( \frac {d \vec L}{dt} \right ) = \vec r \times \vec F ………. (4)
Now, by comparing equations (1) and (4), we will get –
\vec \tau = \left ( \frac {d \vec L}{dt} \right )
Therefore, torque acting on a particle is equal to the rate of change in angular momentum.
Momentum & Moment of Inertia
Consider about a body rotating with angular speed ( \omega ) as shown in figure. Consider that, a particle P of the body of mass ( m_1 ) is at a distance ( r_1 ) from the axis of rotation. Let, its linear velocity is ( v_1 ) .
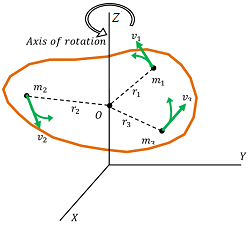
Then, linear momentum of particle is –
p_1 = m_1 v_1 = m_1 ( r_1 ) \omega
Moment of linear momentum of the particle about the ZZ axis is –
L_1 = p_1 r_1 = m_1 ( r_1 )^2 \omega
Similarly, linear momentum of other particles will be L_2 = m_2 ( r_2 )^2 \omega , L_3 = m_3 ( r_3 )^2 \omega etc.
Therefore, angular momentum of the whole body will be –
L = \left ( \Sigma m r^2 \right ) \omega = I \omega
But, \left ( \Sigma m r^2 \right ) represents Moment of Inertia of the body about axis of rotation.
L = I \omega
Therefore, Angular momentum of a rotating body is equal to the product of its moment of inertia about the axis of rotation and angular velocity.
Conservation of Angular Momentum
If total external torque acting on a rigid body is zero, then the total angular momentum of the body is conserved. This is called the law of conservation of angular momentum.
Torque on a particle is given as –
\vec \tau = \left ( \frac {d \vec L}{dt} \right )
When external force or torque is zero, then –
\vec \tau = \left ( \frac {d \vec L}{dt} \right ) = 0
Or, \quad \left ( \frac {d \vec L}{dt} \right ) = 0
This means that, change in momentum of the particle will be zero.
Therefore, \quad L = \text {Constant}
But, \quad L = I \omega . So, \quad I \omega = \text {Constant}
Or, \quad I_1 \omega_1 = I_2 \omega_2
This means that, when no external torque is acting on a body, the angular velocity ( \omega ) of the body can be increased or decreased by decreasing or increasing the moment of inertia of that body.
Examples of this phenomenon are –
- Planetary motion – Planets revolve in elliptical orbit around the sun. When it comes closer to sun, its moment of inertia about the axis through sun decreases. Therefore the angular velocity increases to conserve the angular momentum.
- Rotating turn table – A man carrying heavy weights in his hands and standing on a rotating turn table can decrease the angular speed of turn table by spreading his hands to increase moment of inertia.
See numerical problems based on this article.
