What is a Black Body?
The radiation emitted by a black body is called black body radiation.
A black body is one which neither reflects nor transmits but absorbs whole of the heat radiation incident on it.
A black body has following characteristics –
- Absorptive power of a black body is one. It means a black body absorbs all of the radiation energy incident on its surface.
- Reflective power and transmittive power of a perfect black body are zero.
- When a black body is heated to high temperature, it emits radiations of all possible wavelengths within a certain wavelength range.
Emissive Power
The emissive power of a radiant body at a given temperature and wavelength is defined as the amount of radiant energy of given wavelength emitted per unit time per unit surface area of that body.
Let, a radiant energy ( Q ) of a given wavelength is radiating from a body of surface area ( A ) in time ( t ) .
Then, emissive power of that body will be \quad e = \left ( \frac {Q}{A t} \right )
The SI unit of emissive power is ( J \ s^{- 1} m^{- 2} ) or ( W \ m^{- 2} )
Emissivity
Emissivity of a radiant body is defined as the ratio of the amount of heat energy radiated per unit time per unit surface area of the body in a certain time to the total amount of heat energy emitted by a perfect black body at the same temperature.
Therefore, emissivity ( \epsilon ) of a radiant body is the ratio of emissive power ( e ) of a body to the emissive power ( E ) of a black body at the same temperature.
Thus, \quad \epsilon = \left ( \frac {e}{E} \right )
- Emissivity being a ratio of two similar quantities, it is dimensionless.
- The emissivity of a perfect black body is 1 .
Ferry’s Black Body Radiation
The concept of black body is hypothetical. A perfectly black body can’t be realized in practice. Ferry’s black body is the nearest to a perfect black body.
- A surface coated with lamp black or platinum black can absorbs maximum of ( 95 \ \text {to} \ 97 \% ) of the incident radiation. But on heating it doesn’t emit full radiation spectrum.
- Hence, the concept of ferry’s black body is in existence.
- The nearest example of an ideal black body is Ferry’s black body.
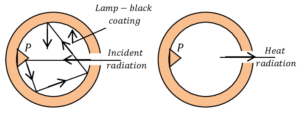
A Ferry’s black body is shown in figure. It has following features –
- It consists of a hollow double walled metal sphere coated inside with lamp black and nickel polished from outside as shown in figure.
- There is a fine hole in it. All radiations entering through this hole is completely absorbed due to multiple reflections as shown in figure.
- The conical projection opposite to the opening prevents direct reflection.
- If this black body is heated to high temperature then it emits radiations of all wavelengths.
- The wavelength range of emitted radiation is independent of the material of the body and depends only on the temperature of the black body.
Kirchoff’s law of Radiation
In radiation mode of heat transfer, Kirchhoff’s thermal radiation law tells about the radiation of certain wavelength emitted or absorbed by a body in thermodynamic equilibrium.
- Kirchoff’s law of radiation consists of two statements.
FIRST STATEMENT –
It states that –
At any given temperature, the ratio of emissive power ( e ) and the absorptive power ( a ) corresponding to a certain wavelength is constant for all surfaces.
Therefore, \left ( \frac {e}{a} \right ) = \text {Constant}
SECOND STATEMENT –
It states that –
At any given temperature, the ratio of emissive power ( e ) and the absorptive power ( a ) corresponding to a certain wavelength is equal to the emissive power ( E ) of a perfectly black body at that temperature to the same wavelength.
Therefore, \quad \left ( \frac {e}{a} \right ) = E
Or, \quad e = E \ a ……… (1)
Also, emissivity ( \epsilon ) of a surface is given by the ratio of emissive power ( e ) of that surface to the emissive power ( E ) of a perfect black body.
\epsilon = \left ( \frac {e}{E} \right ) …….. (2)
Putting the value of ( e = E \ a ) from equation (1) in equation (2), we get –
\epsilon = \left ( \frac {E \ a}{E} \right ) = a
Or, \quad \epsilon = a
Thus, the absorptive power of a body is equal to its emissivity.
- This is another form of Kirchoff’s law.
- Hence, a good absorber is a good emitter and so a poor reflector.
Stefan Boltzmann Law of Radiation
Stefan-Boltzmann law of energy radiation states that –
The total heat energy emitted by a perfect black body per second per unit area is directly proportional to the fourth power of the absolute temperature.
Thus, \quad E \propto T^4 .
Or, \quad E = \sigma T^4 .
If ( H ) is the rate of radiation emitted by a black body of surface area ( A ) , then –
H = EA = \sigma T^4 A
- In ( SI ) units \quad \sigma = 5.67 \times 10^{-8} W m^{-2} K^{-4}
Wien’s Displacement Law
Wien’s displacement law of wavelength of emitted energy states that –
When a black body emits maximum energy, the wavelength of the radiation are inversely proportional to its absolute temperature.
Therefore, \quad \lambda_{max} \propto \left ( \frac {1}{T} \right )
Or, \quad \lambda_{max} T = b
- Here ( b ) is a constant called Wien’s constant.
- Value of Wien’s constant is \quad b = 2.9 \times 10^{-3} m K
EXAMPLE –
- When an iron piece is heated in a hot flame, its colour first becomes dull red, then reddish yellow and finally white.
- This observation is in accordance with the Wien’s law. With increase in temperature the emission of energy is maximum at smaller wave lengths. Because \quad \lambda_{white} < \lambda_{yellow} < \lambda_{red}
See numerical problems based on this article.
