Uniform Circular Motion

What is called a “Uniform Circular Motion”?

Curvilinear motion is the motion of an object along the circumference of a circular path or a curve of any shape or rotation of an object along a circular path. A curvilinear motion can be of following types –

1. Curve motion – A motion along the curvature of a curved path. Example – Motion of a car while taking a turn on curved road.
2. Projectile motion – A motion under the influence of gravity along the parabolic curvature. Example – Trajectory of motion of a javelin thrown in ground.
3. Circular motion –  A motion along the circumference of a circular path. Example – Running of an athlete around a circular ground.
4. Rotary motion – A motion in which a body rotates about its own axis. Example – Rotation of earth about its own axis.

Circular Motion

If a particle moves along a circular path, then it’s motion is called a circular motion. A circular motion is of two types –

1. Non-uniform circular motion – It is the motion of a body moving along a circular path with varying angular acceleration.
2. Uniform circular motion – It is the motion of a body moving along a circular path with constant angular acceleration.

Therefore, if a particle moves along a circular path with a constant speed i.e. it covers equal distances along the circumference of the circle in equal intervals of time, then it’s motion is called a uniform circular motion.

A uniform circular motion is an accelerated motion and concerned acceleration is known as centripetal acceleration.

Most important terms related to a uniform circular motion are –

1. Angular Displacement.
2. Angular velocity.
3. Angular acceleration.
4. Time period.
5. Frequency.

1. Angular Displacement

Consider about a particle moving in a circular path as shown in figure. Let, the particle is initially at point A and after time ( t )  it reaches at the point P .

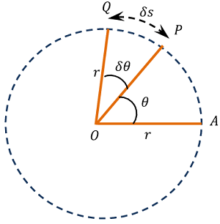
Let, \quad \angle {AOP} = \theta

Now let, Q is the position of the particle after further time ( \delta t ) .

Let, \quad \angle {POQ} = \delta \theta

Then ( \delta \theta ) is called angular displacement of the particle in time ( \delta t ) . It is measured in radians.

2. Angular Velocity

The rate of change of subtended angle ( \theta ) at centre O is called angular velocity of the particle.

From figure, in time ( \delta t ) , the average angular velocity of particle is given by –

\bar {\omega} = \frac {\text {Angular Displacement}}{\text {Time}} = \left ( \frac {\delta \theta}{\delta t} \right )

Therefore, angular velocity of the particle at point P will be –

\omega = \lim\limits_{Q \rightarrow P} \left ( \frac {\delta \theta}{\delta t} \right ) = \left ( \frac {d \theta}{dt} \right )

Therefore, angular velocity ( \omega ) of a particle is the first order derivative of angular displacement ( \theta ) with respect to time.

3. Angular Acceleration

The rate of change of angular velocity is called angular acceleration.

Therefore, Angular acceleration = Rate of change of angular velocity.

Or, \quad \alpha = \left ( \frac {d \omega}{d t} \right ) = \frac {d}{d t} \left ( \omega \right )

Therefore, angular acceleration ( \alpha ) of a particle is the first order derivative of angular velocity ( \omega ) with respect to time.

Again \quad \omega = \left ( \frac {d \theta}{d t} \right )

Therefore, \quad \alpha = \frac {d}{dt} \left ( \frac {d \theta}{dt} \right ) = \left ( \frac {d^2 \theta}{d t^2} \right )

Therefore, angular acceleration ( \alpha ) of a particle is the second order derivative of angular displacement ( \theta ) with respect to time.

Again, \quad \left ( \frac {d \omega}{d t} \right ) = \left ( \frac {d \omega}{d \theta} \right ) \times \left ( \frac {d \theta}{d t} \right ) = \left ( \frac {d \omega}{d \theta} \right ) \omega

Or, \quad \alpha = \omega \left ( \frac {d \omega}{d \theta} \right )

Therefore, angular acceleration ( \alpha ) of a particle is the first order derivative of angular velocity ( \omega ) with respect to angular displacement ( \theta ) .

4. Time period

Time taken by a particle to complete one complete revolution along its circular path is called its period of revolution or Time period.

If time period is denoted by ( T ) , then angular displacement ( \theta ) in time ( T ) will be ( 2 \pi ) radians.

5. Frequency of motion

Number of revolutions per unit time is called frequency.

Therefore, frequency of revolutions is given by –

\nu = \left ( \frac {1}{T} \right )

But, \quad \text {Angular velocity} = \text {Angular displacement per unit time}

We know that, total displacement in one complete revolution is ( \theta = 2 \pi ) radians.

Therefore, \quad \omega = \left ( \frac {\theta}{t} \right ) = \left ( \frac {2 \pi}{T} \right )

= 2 \pi \left ( \frac {1}{T} \right ) = 2 \pi \nu

Where, ( \nu ) is the frequency of revolutions.

Or, \quad \omega = 2 \pi \nu

Relation between Linear & Angular quantities

Very simple relation exist between linear quantities and angular quantities of motion. These are as follows –

Linear Displacement & Angular Displacement 

From figure, in time ( \delta t ) , linear linear displacement of the particle will be ( PQ = ds ) .

We know that, \quad \text {Arc} = \text {Radius} \ \times \ \text {Angle in radians}

Therefore, linear displacement of the particle is –

\delta s = r \times \delta \theta

Therefore, \quad \text {Linear displacement} = \text {Radius} \ \times \ \text {Angular displacement}

Linear Velocity & Angular Velocity

Consider about a particle revolving in a circular path as shown in figure.

Let, the particle describes a circle of radius, ( r ) with constant linear speed, ( v ) and angular velocity ( \omega ) .

Let, A  is the position of particle at any instant and P  is the position after one second. Then length of arc ( AP ) is the actual distance traveled in one second which is called linear velocity ( v )

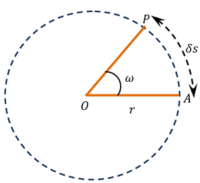
Also angular velocity of particle \quad \angle {AOP} = \omega radians.

But \quad \left ( \frac {\text {Arc  AP}}{OA} \right ) = \angle {AOP} in radians.

Now, linear velocity \quad v = \left ( \frac {ds}{dt} \right )

But, \quad ds = ( r \times d \theta )

Therefore, \quad v = \left ( \frac {r \times d \theta}{dt} \right ) = \left ( r \times \omega \right )

Or, \quad v = \omega r

Therefore, \quad \text {Linear velocity} = \text {Radius} \ \times \ \text {Angular velocity}

Linear Acceleration & Angular Acceleration

We know that, \quad v = \omega r

Differentiating this equation with respect to time, we will get –

\left ( \frac {dv}{dt} \right ) = r \left ( \frac {d \omega}{dt} \right )

But, \quad \left ( \frac {dv}{dt} \right ) = a \quad and \quad \left ( \frac {d \omega}{dt} \right ) = \alpha

Therefore, \quad a = r \alpha

Therefore, \quad \text {Linear acceleration} = \text {Radius} \ \times \ \text {Angular acceleration}

Planer or Curvilinear Motion

Out of three coordinates, if two co-ordinates are required to specify the position of a moving object, then the motion of the object is called a curvilinear motion.

It is a two dimensional motion which is commonly known as a planer motion.

Examples –

1. Motion of planets around the sun.
2. A car moving in a curved path.
3. Circular motion etc.

See numerical problems based on this article.

• P030109
• P030115
• P030124
• P090109
• P090110