Friction on Inclined plane

How Friction acts on Inclined Plane?

Friction on an inclined plane depends upon the angle of inclination of the plane. As the angle of inclination increases, the friction force decreases.

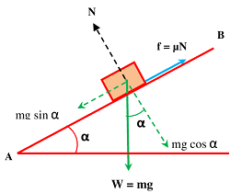
To understand this, consider about a solid block resting on an adjustable inclined plane AB as shown in figure. Let, mass of the block is ( m ) and inclination of the plane to the horizontal is ( \alpha ) .

At this situation, rectangular components of weight of body are –

1. Parallel to the inclined plane is ( mg \sin \alpha ) .
2. Perpendicular to the inclined plane is ( mg \cos \alpha ) .

The component ( mg \sin \alpha ) acting parallel to the inclined plane helps in moving the body downwards but the body remains in rest due to developed friction ( f ) .

Now, inclination of plane ( \alpha ) is gradually increases. Due to increase in inclination, an instance achieved when the block is in a state of just to move down.

At this instant the body is is equilibrium due to the effect of following forces –

• Component of weight of body in a direction parallel to the plane is ( mg \sin \alpha ) . It is acting downwards.
• Force of friction at the contact surfaces of body and plane. Since body has a tendency to move down the plane, hence friction force will be acting upward.
• Normal reaction ( f ) in a direction perpendicular to plane.

Since the body is in rest, so for equilibrium of the body –

N = mg \cos \alpha

Thus, normal reaction acting on the contact surface depends on angle of inclination of inclined plane.

Also, \quad f  =  mg \sin \alpha

From geometry of the figure, we have –

• Angle between normal reaction ( N ) and weight of body ( W = mg ) is ( 180 \degree - \alpha ) .
• Angle between friction force ( f ) and weight no body ( W = mg ) is ( 90 \degree + \alpha ) .

By applying lami’s theorem for the forces, we get –

\left [ \frac {N}{\sin \left (90 \degree + \alpha \right )} \right ] = \left [ \frac {f}{\sin \left (180 \degree - \alpha \right )} \right ]

But, \quad f  = \mu N 

In this way, as the angle of inclination increases, normal reaction ( N ) decreases so friction decreases also.

Angle of Inclination and Angle of Friction

By applying lami’s theorem for the forces acting on body, we get –

\left [ \frac {N}{\sin \left (90 \degree + \alpha \right )} \right ] = \left [ \frac {\mu N}{\sin \left (180 \degree - \alpha \right )} \right ]

So, \quad \left ( \frac {N}{\cos \alpha} \right ) = \left ( \frac {\mu N}{\sin \alpha} \right )

Or, \quad \left ( \frac {\sin \alpha}{\cos \alpha} \right ) = \left ( \frac {\mu N}{N} \right )

Therefore, \quad \tan \alpha = \mu

But, from the definition of coefficient of friction, we have –

\mu = \tan \phi

Therefore, \quad \tan \alpha = \tan \phi

Or, \quad \alpha = \phi

Therefore, at limiting condition, the angle of inclination of plane is just equal to the angle of friction for the inclined plane.

Friction during motion down an Inclined Plane

Consider about a body as shown in figure. Let, the angle of inclination of plane increases and a pull ( P ) is applied at an angle ( \theta ) to the plane, to keep the body in equilibrium.

Now resolving the pulling force in rectangular components, we get –

• Effect of pull in the direction perpendicular to the plane is ( P \sin \theta )
• Effect of pull in the direction parallel to the plane is ( P \cos \theta )

Consider that, the pull is not sufficient and the body has a tendency to slide down the plane.

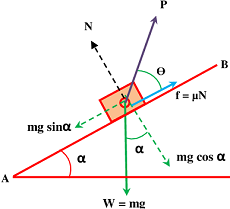
At this situation, from geometry of figure, we get –

( P \cos \theta + f ) = mg \sin \alpha

So, \quad ( P \cos \theta + \mu \ N ) = mg \sin \alpha

And, \quad ( N + P \sin \theta ) = mg \cos \alpha

So, \quad N = ( mg \cos \alpha - P \sin \theta )

Eliminating ( N ) from above equations, we get –

P \cos \theta + \mu \left (mg \cos \alpha - P \sin \theta \right ) ] = mg \sin \alpha .

Or, \quad [ P \left ( \cos \theta - \mu \sin \theta \right ) ] = [ mg \left ( \sin \alpha - \mu \cos \alpha \right ) ]

So, \quad P = \left [ \frac { mg \left ( \sin \alpha - \mu \cos \alpha \right )}{ \left ( \cos \theta - \mu \sin \theta \right )} \right ]

But, \quad \mu = \tan \phi \quad

Therefore, \quad P = \left [ \frac {mg \left ( \sin \alpha - \tan \phi \cos \alpha \right )}{\left ( \cos \theta - \tan \phi \sin \theta \right )} \right ]

Multiplying numerator and denominator by ( \cos \phi ) , we get –

P = \left [ \frac {mg \left ( \sin \alpha \cos \phi - \sin \phi \cos \alpha \right )}{\left ( \cos \theta \cos \phi - \sin \phi \sin \theta \right )} \right ]

= \left [ \frac {mg \sin \left ( \alpha - \phi \right )}{\cos \left ( \theta + \phi \right )} \right ]

Solving this equation, we can get the minimum value of pulling force ( P ) which is necessary to hold the body in equilibrium.

Friction during motion up an Inclined Plane

Now consider that, the pulling force ( P ) is just sufficient and the body is just at point of motion up the plane. Hence the force of friction will act downward.

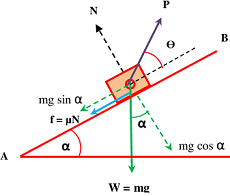
In this condition, for equilibrium of body –

P \cos \theta = ( f + m g \sin \alpha )

= ( \mu \ N + m g \sin \alpha )

And \quad ( N + P \sin \theta ) = m g \cos \alpha

So, \quad N = ( m g \cos \alpha - P \sin \theta )

Eliminating ( N ) from above equations we get –

P \cos \theta = [ \mu \left ( m g \cos \alpha - P \sin \theta \right ) + m g \sin \alpha ]

So, \quad P \left ( \cos \theta + \mu \sin \theta \right ) = mg \left ( \sin \alpha + \mu \cos \alpha \right )

Or, \quad P = \frac { m g \left ( \sin \alpha + \mu \cos \alpha \right )}{ \left ( \cos \theta + \mu \sin \theta \right )}

But, \quad \mu = \tan \phi

Therefore, \quad P = \left [ \frac { m g \left ( \sin \alpha + \tan \phi \cos \alpha \right )}{ \left ( \cos \theta + \tan \phi \sin \theta \right )} \right ]

Multiplying numerator and denominator by ( \cos \phi ) we get –

P = \left [ \frac { m g \left ( \sin \alpha \cos \phi + \sin \phi \cos \alpha \right )}{ \left ( \cos \theta \cos \phi + \sin \phi \sin \theta \right )} \right ]

= \left [ \frac {mg \sin \left ( \alpha + \phi \right )}{\cos \left ( \theta - \phi \right )} \right ]

In this expression ( P ) will be minimum when numerator will be minimum or denominator will be maximum. But ( mg ), \ ( \alpha ) \ \text {and} \ ( \phi ) , all are constants. Hence, numerator \left [ mg \sin ( \alpha + \phi ) \right ] is also a constant term.

Therefore, for ( P ) to be minimum, denominator [ \cos ( \theta  –  \phi ) ] , should be maximum.

We know that, maximum value of ( \cos \theta ) is 1 . But ( 1 = \cos 0 \degree ) . This maximum value of \left [ \cos ( \theta – \phi ) \right ] = 1 will arise when [ ( \theta – \phi ) = 0 ]

Therefore, \quad [ ( \theta – \phi ) = 0 \degree ]

So, \quad \theta = \phi

Putting the value of ( \theta = \phi ) in the expression for ( P ) , we get –

P_{Minimum} = mg \sin \left ( \alpha + \phi \right )

Therefore, minimum pull required to draw a body up an inclined plane is \left [ mg \sin ( \alpha + \phi ) \right ] which is required to apply in a direction inclined at an angle equal to the angle of friction, i.e. ( \theta = \phi )

Friction in Inclined Plane (when force act horizontal)

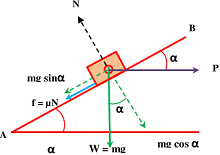
Consider about the figure as shown. Let, the pull ( P ) is applied horizontally.

When the body is just to move upward –

By, parallelogram law of forces, we have –

P \cos \alpha = ( mg \sin \alpha + \mu N )

And, \quad N = ( P \sin \alpha + mg \cos \alpha )

Eliminating ( N ) from above equations, we get –

P \cos \alpha = \left [ mg \sin \alpha + \mu \left ( mg \cos \alpha + P \sin \alpha \right ) \right ]

Or, \quad P \left ( \cos \alpha - \mu \sin \alpha \right ) = mg \left ( \sin \alpha + \mu \cos \alpha \right )

So, \quad P = \left [ \frac {mg \left ( \sin \alpha + \mu \cos \alpha \right )}{ \left ( \cos \alpha - \mu \sin \alpha \right )} \right ]

= \left [ \frac {mg \left ( \sin \alpha + \tan \phi \cos \alpha \right )}{ \left ( \cos \alpha - \tan \phi \sin \alpha \right )} \right ]

Multiplying numerator and denominator by ( \cos \phi ) , we get –

P = \left [ \frac {mg \left ( \sin \alpha \cos \phi + \sin \phi \cos \alpha \right )}{ \left ( \cos \alpha \cos \phi - \sin \phi \sin \alpha \right )} \right ]

= \left [ \frac {mg \sin \left ( \alpha + \phi \right )}{ \cos \left ( \alpha + \phi \right )} \right ] = \left [ mg \tan \left ( \alpha + \phi \right ) \right ]

When the body is just to move downward –

In this case, \quad P \cos \alpha = ( mg \sin \alpha - \mu N )

And, \quad N = ( P \sin \alpha + mg \cos \alpha )

Solving the equations by the procedures discussed above, we get –

P = \left [ mg \tan \left ( \alpha - \phi \right ) \right ]

Therefore, following conclusions are made from above equations –

When ( \alpha > \phi ) ( i.e. angle of inclination is greater than the angle of friction ) then, the required pull ( P ) is positive i.e. it is in the direction shown in the figure above. Therefore, an effort of magnitude [mg \tan ( \alpha + \phi ) ] will require to move the block up the plane.

When ( \alpha < \phi ) ( i.e. angle of inclination is lower than the angle of friction ) then, the required pull ( P ) is negative i.e. it is in the opposite direction of the direction shown in figure above. Therefore, an effort of magnitude [mg \tan ( \alpha - \phi ) ] will be required to move the block down the plane.