How Electric Field is produced by a Charged Shell?
Gauss law helps in evaluating the electric field of bodies having continuous charge distribution like a charged wire, charged thin sheet, charged sphere etc. Hence, to find the electric field of shell, we use Gauss law.
Consider that a positive charge ( + q ) is distributed uniformly on the surface of a spherical shell of radius ( R ) . Using Gauss law, let us find the electric field at following points –
- Electric field at a point outside the shell.
- Electric field at a point on the surface of shell.
- Electric field at a point inside the shell.
Electric Field at an outside point of Charged Shell
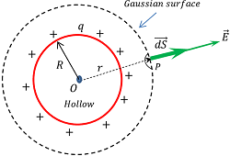
Consider about a point P at a distance ( r ) from the centre of the shell. In this case \left ( r > R \right ) .
We will draw a Gaussian surface in the form of a sphere of radius ( r ) and centre at O . Then according to Gauss law –
\oint\limits_{S} \vec {E} \ d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad \oint\limits_{S} E d S \cos \theta = \left ( \frac {q}{\epsilon_0} \right ) ……. (1)
Since, ( \vec {E} ) and ( \vec {S} ) are along the same direction, so ( \theta = 0 \degree ) . Therefore –
\oint\limits_{S} E d S \cos 0 \degree = \left ( \frac {q}{\epsilon_0} \right )
So, \quad \oint\limits_{S} E d S = \left ( \frac {q}{\epsilon_0} \right )
Since, chosen Gaussian surface is symmetrical about the spherical shell, hence electric field intensity is constant at every point of the Gaussian surface.
So, \quad E \int\limits_{S} dS = \left ( \frac {q}{\epsilon_0} \right ) ……… (2)
But, \quad \int\limits_{S} dS = 4 \pi r^2 (Surface area of Gaussian surface).
Therefore, \quad E \times 4 \pi r^2 = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2} \right ) ……… (3)
Thus, electric field due to a uniformly charged thin spherical shell is such that if the whole charge is concentrated at the centre of the shell.
Electric Field at outside surface of a Charged Shell
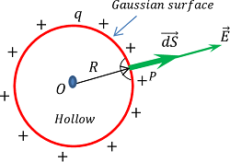
Consider about a point P on the surface of shell. Then ( r = R )
Putting the value of ( r = R ) in equation (3), we will get –
E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{R^2} \right ) ……… (4)
Let, ( \sigma ) is the surface charge density for the spherical shell.
Then, \quad q = \sigma \left ( 4 \pi R^2 \right )
Therefore, \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {\sigma \times 4 \pi R^2}{R^2} \right )
= \left ( \frac {\sigma}{\epsilon_0} \right ) ……… (5)
Electric Field inside Shell
Consider about a point P inside the shell. Then ( r < R ) . We will draw a Gaussian surface of radius ( r ) and centre point at O .Then, according to Gauss law –
\oint\limits_{S} \vec {E} . d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
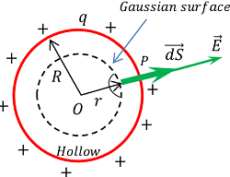
Charge is distributed on the surface of the shell. Inside the shell there is no charge. Hence charge enclosed by the Gaussian surface will be zero i.e. ( q = 0 ) .
Therefore, \quad \oint\limits_{S} \vec {E} . d \vec {S} = 0
Or, \quad E = 0 ………. (6)
Thus there is no electric field inside the charged spherical shell.
Variation of Electric Field of Shell
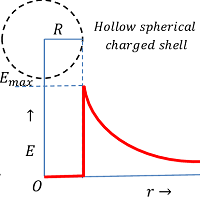
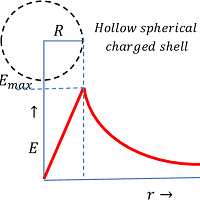
Variation of electric field at various points about a charged spherical shell is shown in figure. It is to be noted that –
- When, ( r < R ) \quad then \quad E = 0
- When, ( r = R ) \quad then \quad E = \left ( \frac {\sigma}{\epsilon_0} \right ) = E_{max} ( Maximum possible value ).
- When, ( r > R ) \quad then \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2} \right )
Thus, electric field intensity is zero inside the shell, maximum at the surface and then varies inversely proportional to the square of distance from centre of the shell as shown in figure.
See numerical problems based on this article.
Electrical Field by a charged Solid Sphere
Consider that a positive charge (+ q ) is distributed uniformly on the surface of a solid sphere of radius ( R ) .
Using Gauss law, let us find the electric field at following points –
- Electric field at a point outside the sphere.
- Electric field at a point on the surface of sphere.
- Electric field at a point inside the sphere.
Electric Field at a point outside of Sphere
Consider about a point P at a distance ( r ) from the centre of sphere. Here, ( r > R ) . We will draw a Gaussian surface in the form of a sphere of radius ( r ) and centre point at O . Then according to Gauss law –
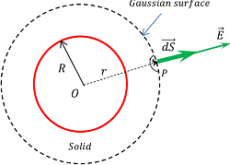
\oint\limits_{S} \vec {E} . d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad \oint\limits_{S} E d S \cos \theta = \left ( \frac {q}{\epsilon_0} \right )
Since, ( \vec {E} ) and ( \vec {S} ) are along the same direction, so ( \theta = 0 \degree )
Therefore, \quad \oint\limits_{S} E d S \cos 0 \degree = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad \oint\limits_{S} E d S = \left ( \frac {q}{\epsilon_0} \right )
Since, Gaussian surface is symmetrical about the charged sphere, hence electric field intensity is constant at every point of the Gaussian surface.
So, \quad E \int\limits_{S} dS = \left ( \frac {q}{\epsilon_0} \right ) ……… (1)
But, \quad \int\limits_{S} dS = \left ( 4 \pi r^2 \right ) (Surface area of Gaussian surface).
Therefore, \quad E \times 4 \pi r^2 = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2} \right ) ……… (2)
Thus electric field due to a uniformly charged solid sphere is such that if the whole charge is concentrated at the centre of the solid sphere.
Electric Field at surface of Sphere
Consider about a point P on the surface of sphere. Then, ( r = R )
Therefore, putting ( r = R ) in equation (2) we will get –
E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{R^2} \right ) ……… (3)
But, \quad q = \rho \left ( \frac {4}{3} \pi R^3 \right )
Where, ( \rho ) is the volume charge density for the sphere.
Therefore, \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {\rho \times \frac {4}{3} \pi R^3}{R^2} \right )
= \left ( \frac {\rho}{3 \epsilon_0} \right ) R ………. (4)
Electric Field at inside of Sphere
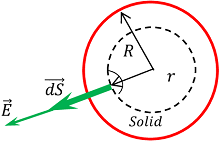
Consider about a point P inside the sphere. Then, ( r < R )
We will draw a Gaussian surface of radius ( r ) and centre at O .
Assume that, charge is uniformly distributed over the entire volume of sphere of radius ( R ) , then charge enclosed by Gaussian surface will be –
q' = q \times \frac {Volume \ of \ Gaussian \ sphere \ of \ radius \ r}{Volume \ of \ charged \ sphere \ of \ radius \ R}
Therefore, \quad \quad q' = q \left ( \frac {1}{\frac {4}{3} \pi R^3} \right ) \times \left ( \frac {4}{3} \pi r^3 \right ) = q \left ( \frac {r^3}{R^3} \right ) .
According to Gauss law –
\oint\limits_{S} \vec {E} . d \vec {S} = \left ( \frac {q'}{\epsilon_0} \right ) = \left ( \frac {1}{\epsilon_0} \right ) q \left ( \frac {r^3}{R^3} \right )
Or, \quad E dS \cos \theta = \left ( \frac {q r^3}{\epsilon_0 R^3} \right )
Since, ( \vec {E} ) and ( \vec {S} ) are along the same direction, so ( \theta = 0 \degree )
Therefore, \quad \oint\limits_{S} E d S \cos 0 \degree = \left ( \frac {qr^3}{\epsilon_0 R^3} \right )
Or, \quad \oint\limits_{S} E d S = \left ( \frac {qr^3}{\epsilon_0 R^3} \right )
Since, chosen Gaussian surface is symmetrical about the charged sphere, hence electric field intensity is constant at every point of the Gaussian surface.
So, \quad E \int\limits_{S} dS = \left ( \frac {qr^3}{\epsilon_0 R^3} \right )
But, \quad \int\limits_{S} dS = \left ( 4 \pi r^2 \right ) ( Surface area of spherical Gaussian surface ).
Therefore, \quad E \times \left ( 4 \pi r^2 \right ) = \left ( \frac {qr^3}{\epsilon_0 R^3} \right )
Or, \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {qr}{R^3} \right )
Therefore, \quad E \propto r
Thus electric field at a point inside the sphere is directly proportional to distance of point from centre of sphere.
Variation of Electric Field in Sphere
Variation of electric field intensity at various points of a charged sphere is shown in figure. It should be noted that –
- When, ( r < R ) \quad then \quad E \propto R
- When, ( r = 0 ) \quad then \quad E = 0 ( Field intensity is zero at the centre of sphere ).
- When, ( r = R ) \quad then \quad E = \left ( \frac {\rho}{3 \epsilon_0} \right ) R = E_{max} ( Maximum possible value of field intensity ).
- When, ( r > R ) \quad then \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2} \right )
Thus, electric field intensity is zero inside the sphere, maximum at the surface and then varies inversely proportional to the square of distance from centre as shown in figure.
See numerical problems based on this article.
