What is Bernoulli’s theorem?
Bernoulli’s theorem states that –
“Total energy of a liquid particle in a perfect in-compressible liquid flowing in a continuous stream in a pipe remains constant.”
- Bernoulli’s theorem is associated with the energy of a flowing fluid.
- Bernoulli’s theorem statement is based on the assumption that, there are no energy loss due to friction in the pipe.
Therefore, according to the Bernoulli’s statement –
\quad \left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) = \text {Constant} .
Or, \quad \text {Total energy of liquid} = \text {Potential energy} \ ( Z ) + \text {Pressure energy} \left ( \frac {p}{w} \right ) + \text {Kinetic energy} \left ( \frac {v^2}{2 g} \right ) = \text {Constant} .
Energy of a fluid
Energy of a fluid body is defined as its capacity of doing work.
A fluid body can possess various forms of energies of which the following types of energies are most important.
- Potential energy.
- Pressure energy.
- Kinetic energy.
Potential energy
Potential energy is the energy possessed by a fluid body by virtue of its position or location in space.
Consider about ( W ) kg of a fluid kept at a height of ( Z ) meters above a datum line. The potential energy of that fluid will be equal to ( WZ ) \ \text {kg-m}
Thus, the potential energy per kg of the fluid body will be –
\left ( \frac {W Z}{W} \right ) \left ( \frac {\text {kg-m}}{\text {kg}} \right ) = Z \ \text {mtr.} .
- We can say that, pressure head due to potential energy of the fluid is ( Z ) \ \text {mtr.}
Pressure energy
Pressure energy is the energy possessed by a fluid by virtue of the pressure at which it is maintained.
Consider that, ( W ) kg of a fluid body is under a pressure of ( p ) \ \text {kg-m}^{-2} . Then the pressure energy of the fluid will be –
W \left ( \frac {p}{w} \right ) \ \text {kg} \left ( \frac {\text {kg-m}^{-2}}{\text {kg-m}^{-3}} \right ) = W \left ( \frac {p}{w} \right ) \ \text {kg-m}
Where ( w ) is the specific weight of the fluid in \text {kg-m}^{-3} .
Therefore, pressure head per kg of the fluid under pressure will be \left ( \frac {p}{w} \right ) \ \text {mtr.}
- We can say that, pressure head due to pressure energy of the fluid is \left ( \frac {p}{w} \right ) \ \text {mtr.}
Kinetic energy
Kinetic energy is the energy possessed by a fluid body by virtue of its motion.
Consider that, ( W ) kg of a fluid is moving at a velocity of ( v ) \text {m-s}^{-1} .
Then, the kinetic energy of fluid will be –
W \left ( \frac {v^2}{2 g} \right ) \ \text {kg-m}
Therefore, kinetic energy per kg of the fluid body will be –
\left ( \frac {v^2}{2 g} \right ) \ \text {mtr.}
- We can say that, pressure head due to kinetic energy of the fluid is \left ( \frac {v^2}{2 g} \right ) \ \text {mtr.}
Total energy
If a fluid body of weight ( W ) \ \text {kg} is at a height of ( Z ) \ \text {mtr.} above a datum line, and at a pressure intensity of ( p ) \ \text {kg-m}^{-2} and moving with a velocity of ( v ) \ \text {m-s}^{-1} , then the total energy of the fluid body will be –
W \left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) \ \text {kg-m}
Therefore, total energy per kg of the fluid body will be –
\left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) \ \text {mtr.}
- We can say that, the pressure head due to total energy is –
\left ( Z + \frac {p}{w} + \frac {v^2}{2 g} \right ) \ \text {mtr.}
- It is also known as total energy head.
Equation of cotinuity
Consider about a perfect in-compressible liquid flowing through a non-uniform pipeline as shown in figure. In this, consider about two sections AA \text {and} BB of the pipe. Assume that, the pipe is running full and there is a continuity of flow between the two sections.
Let –
- ( Z_1 ) is height of section AA above the datum line.
- ( p_1 ) is pressure of fluid at section AA .
- ( v_1 ) is velocity of liquid at section AA .
- ( a_1 ) is area of cross section of the pipe at section AA .
And Z_2, \ p_2, \ v_2, \ a_2 are the corresponding values at section BB .
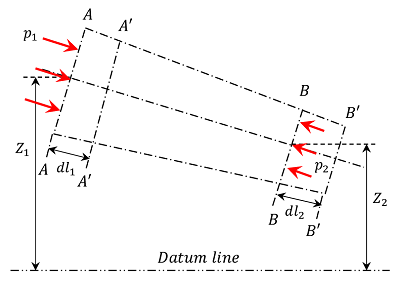
Let, the liquid between the two sections AA \ \text {and} \ BB move to sections A'A' \ \text {and} \ B'B' .
Let, the length of pipe between the sections AA \ \text {and} \ A'A' is ( dl_1 ) and between sections BB \ \text {and} \ B'B' is ( dl_2 ) as shown in figure.
This movement of liquid between AA \ \text {and} \ BB is equivalent to the movement of the liquid particles between AA \ \text {and} \ A'A' \ \text {to} \ BB \ \text {and} \ B'B' , the remaining liquid between sections A'A' \ \text {and} \ BB remains unaffected.
Let, ( W ) is the weight of the liquid between AA \ \text {and} \ A'A' .
We can apply Bernoulli’s theorem in the flow of liquid between the sections AA \ \text {and} \ BB
- Since the flow is continuous, therefore –
W = w \ a_1 \ dl_1 = w \ a_2 \ dl_2
Or, \quad a_1 \ dl_1 = \frac {W}{w} \quad \text {and} \quad a_2 \ dl_2 = \frac {W}{w}
Therefore, \quad a_1 \ dl_1 = a_2 \ dl_2
Expression for Bernoulli’s equation
- Work done by the pressure ( p_1 ) at AA , in moving the liquid from AA \ \text {to} \ A'A' is –
\text {Force} \times \text {Distance} = ( p_1 \ a_1 ) \times dl_1
- Similarly, work done by pressure at BB in moving the liquid from BB \ \text {to} \ B'B' is –
\text {Force} \times \text {Distance} = - ( p_2 \ a_2 ) \times dl_2
Minus sign is taken as the direction of ( p_2 ) is opposite to that of ( p_1 ) .
- Total work done by the fluid pressure will be –
( p_1 \ a_1 ) dl_1 - ( p_2 \ a_2 ) dl_2
Or, \quad p_1 \ a_1 \ dl_1 - p_2 \ a_2 \ dl_2
By substituting \quad ( a_2 \ dl_2 ) = ( a_1 \ dl_1 ) , we get –
- Work done by the fluid pressure is –
p_1 \ a_1 \ dl_1 - p_2 \ a_1 \ dl_1 = a_1 \ dl_1 ( p_1 - p_2 )
= \frac {W}{w} ( p_1 - p_2 )
- Loss of potential energy in moving the fluid from AA \ \text {to} \ BB is –
W ( Z_1 - Z_2 )
- And gain in kinetic energy in moving the fluid from AA \ \text {to} \ BB is –
W \left ( \frac {v_2^2}{2g} - \frac {v_1^2}{2g} \right ) = \frac {W}{2g} \left ( v_2^2 - v_1^2 \right )
By principle of conservation of energy, we know that –
\text {Loss of potential energy} + \text {Work done by pressure} = \text {Gain in kinetic energy}
Therefore, \quad W ( Z_1 - Z_2 ) + \frac {W}{w} ( p_1 - p_2 ) = \frac {W}{2g} ( v_2^2 - v_1^2 )
Or, \quad ( Z_1 - Z_2 ) + \frac {p_1}{w} - \frac {p_2}{w} = \frac {v_2^2}{2g} - \frac {v_1^2}{2g}
Or, \quad Z_1 + \frac {p_1}{w} + \frac {v_1^2}{2g} = Z_2 + \frac {p_2}{w} + \frac {v_2^2}{2g}
